编译原理
编译原理
2023 - 2024 春夏
Introduction
2024.02.29
compiler: 一个将一种语言翻译为另一种语言的程序 ( 语言与计算机相关 )。
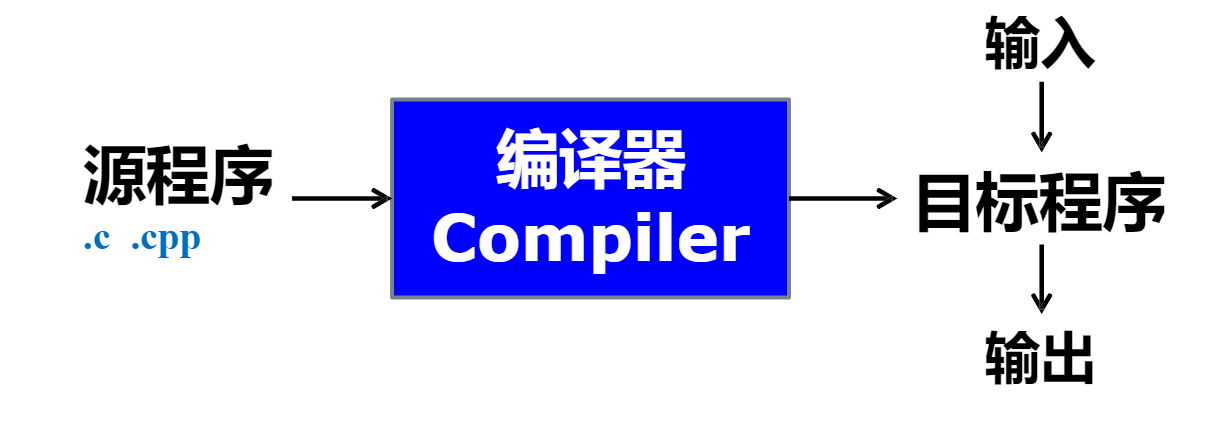
Typical Workflow of a Compiler
编译器的工作阶段通常如下:分为前、中、后三端
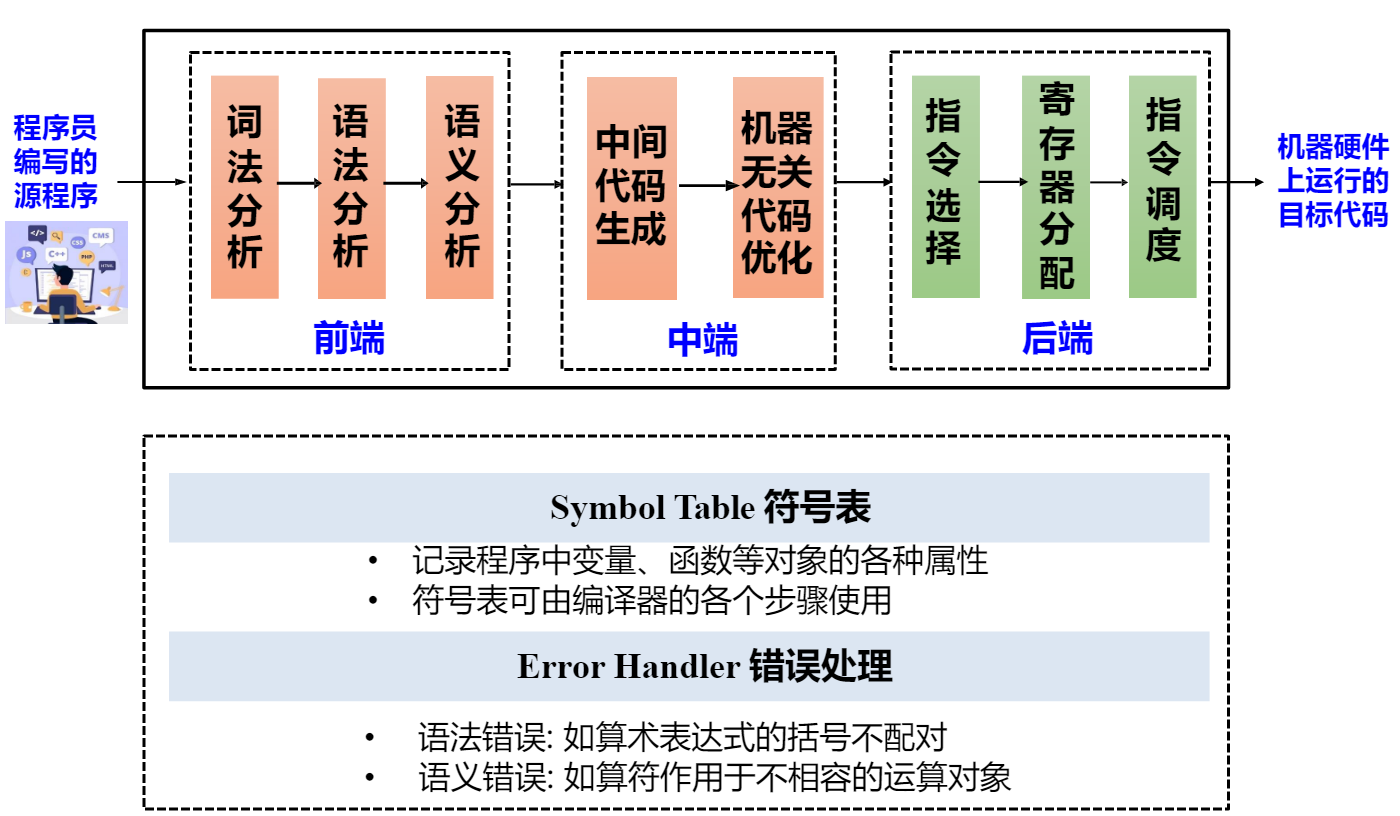
-
词法分析 (Lexical Analysis): String \(\rightarrow\) token sequence ( 记号序列 ),删除不必要的部分。通常使用正则表达式定义 ( 例如
rm 2024*),用于匹配不同的 token。 -
语法分析 (Syntactic Analysis): 将记号序列解析为某种语法结构 ( 如语法树 )。
-
语义分析 (Semantic Analysis): 分析语法树节点的属性信息等。得到符号表等。
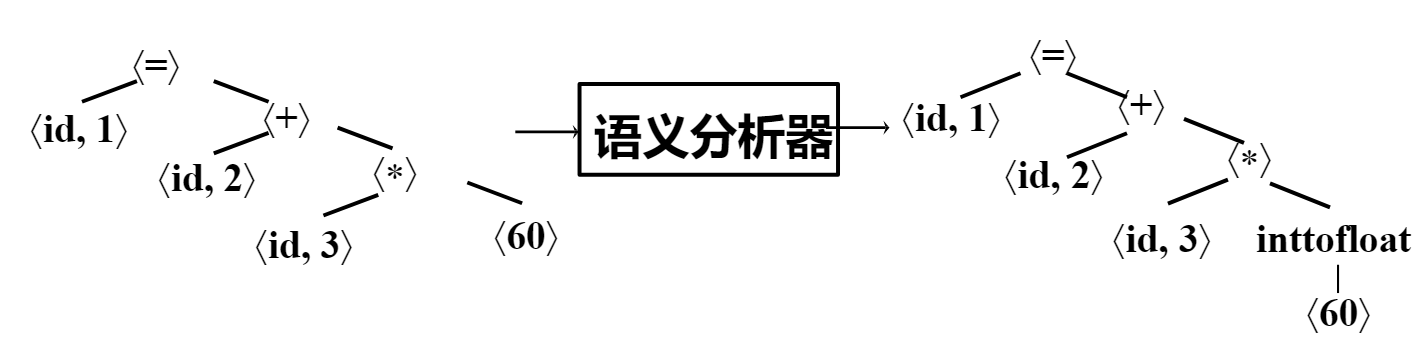
- 中间代码生成 (IR): 源语言与目标语言的桥梁。( 三地址 : 每个表达式中至多一个操作符两个操作数 )
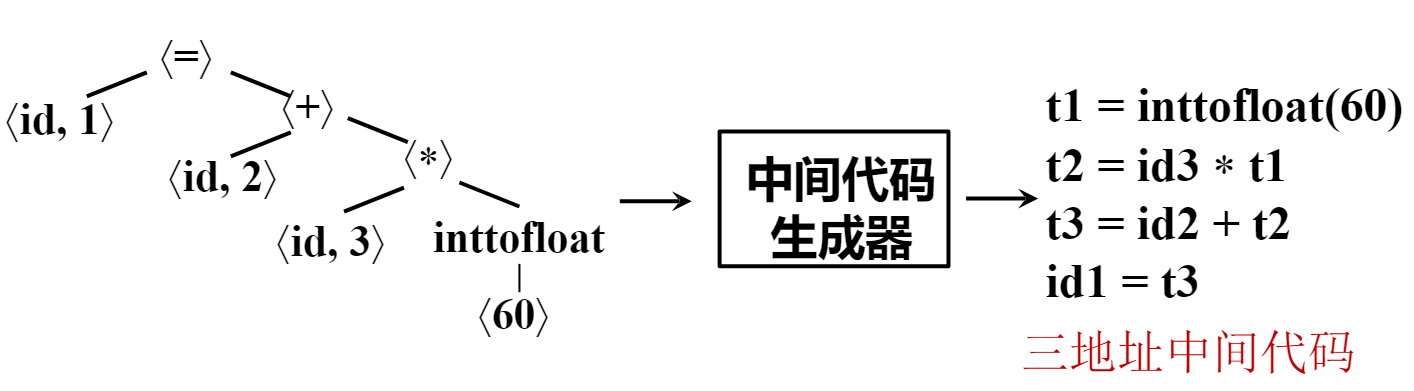
- ** 基于中间表示的优化 ** ( 机器无关代码优化 ): 对中间代码进行优化和变换,降低执行时间,减少资源消耗。
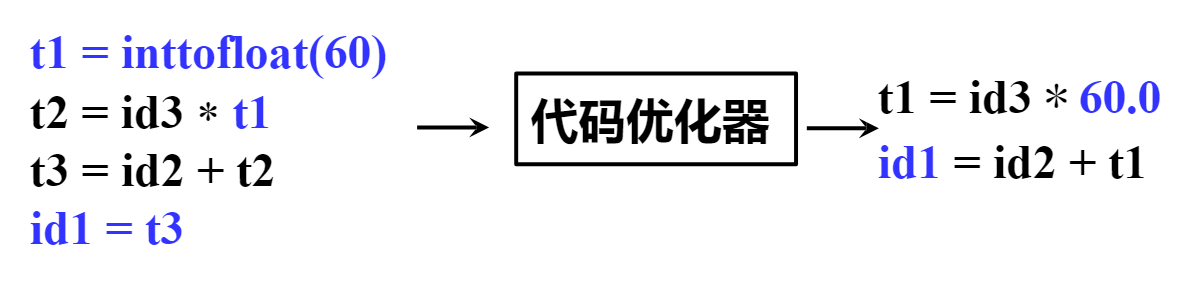
- 后端 - 目标代码生成 : 把中间代码翻译为目标语言,涉及到指令选择、寄存器分配、指令调度等。
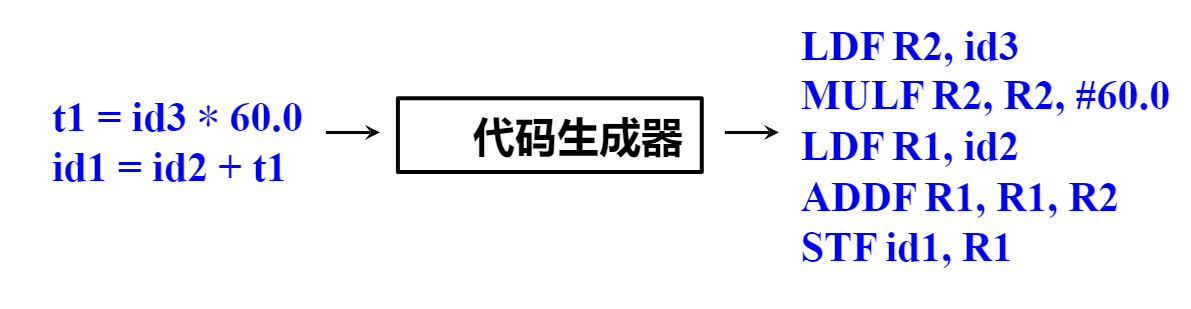
Tiger 编译器
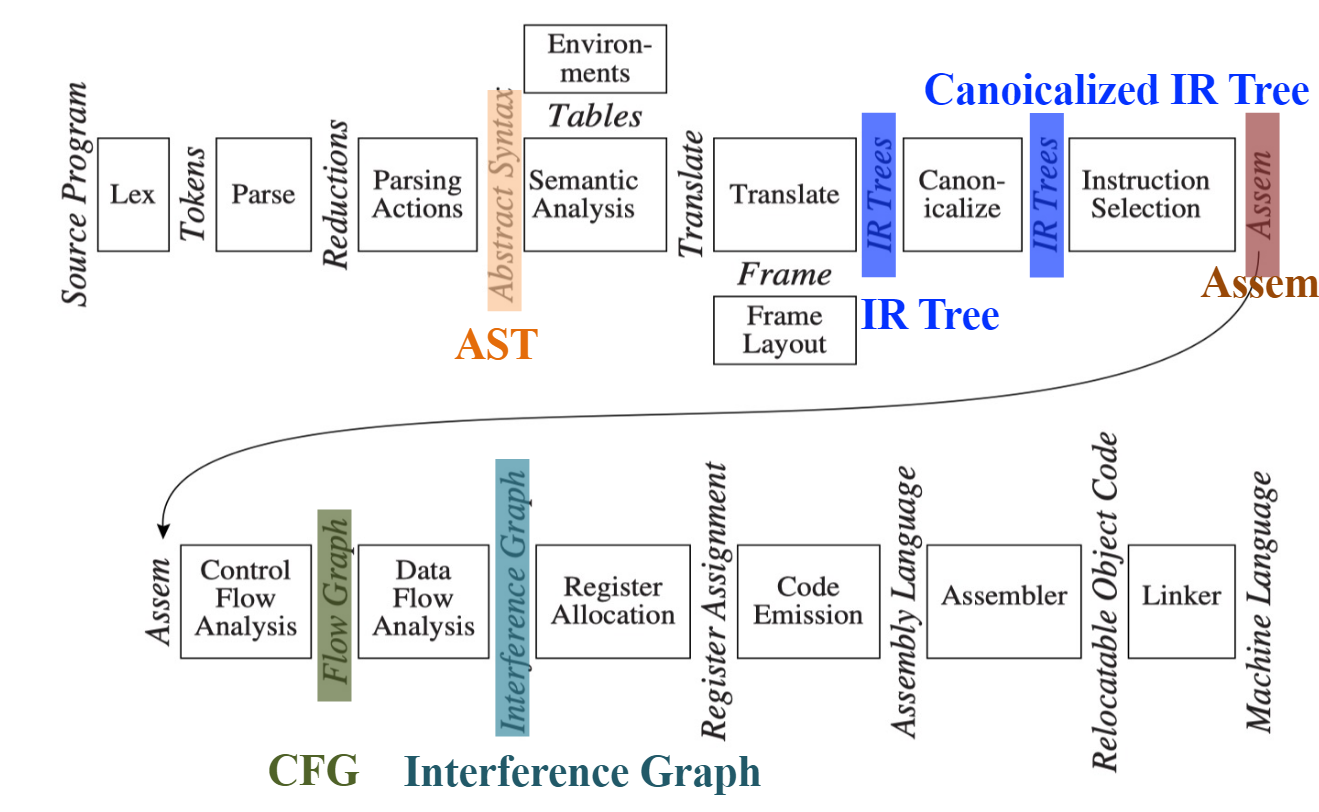
- AST ( 抽象语法树 ): 经过语法分析 + "Parsing Actions" 生成。
- IR Tree ( 树型中间表示 ): 语义分析之后按照一定规则生成。进行了归一化 (Canonicalized) 的操作。
- Control Flow Analysis ( 控制流分析 ): 判断分支语句的执行路径 ( 可以去除不可达的路径 )。
- CFG (Control Flow Graph) ( 控制流图 ): 方便进行数据流分析–如活跃变量分析 (Liveness Analysis)。
- Interference Graph ( 冲突图 ): 从活跃变量分析的结果构造,用于指导寄存器分配。
Lexical Analysis 词法分析
2024.03.07
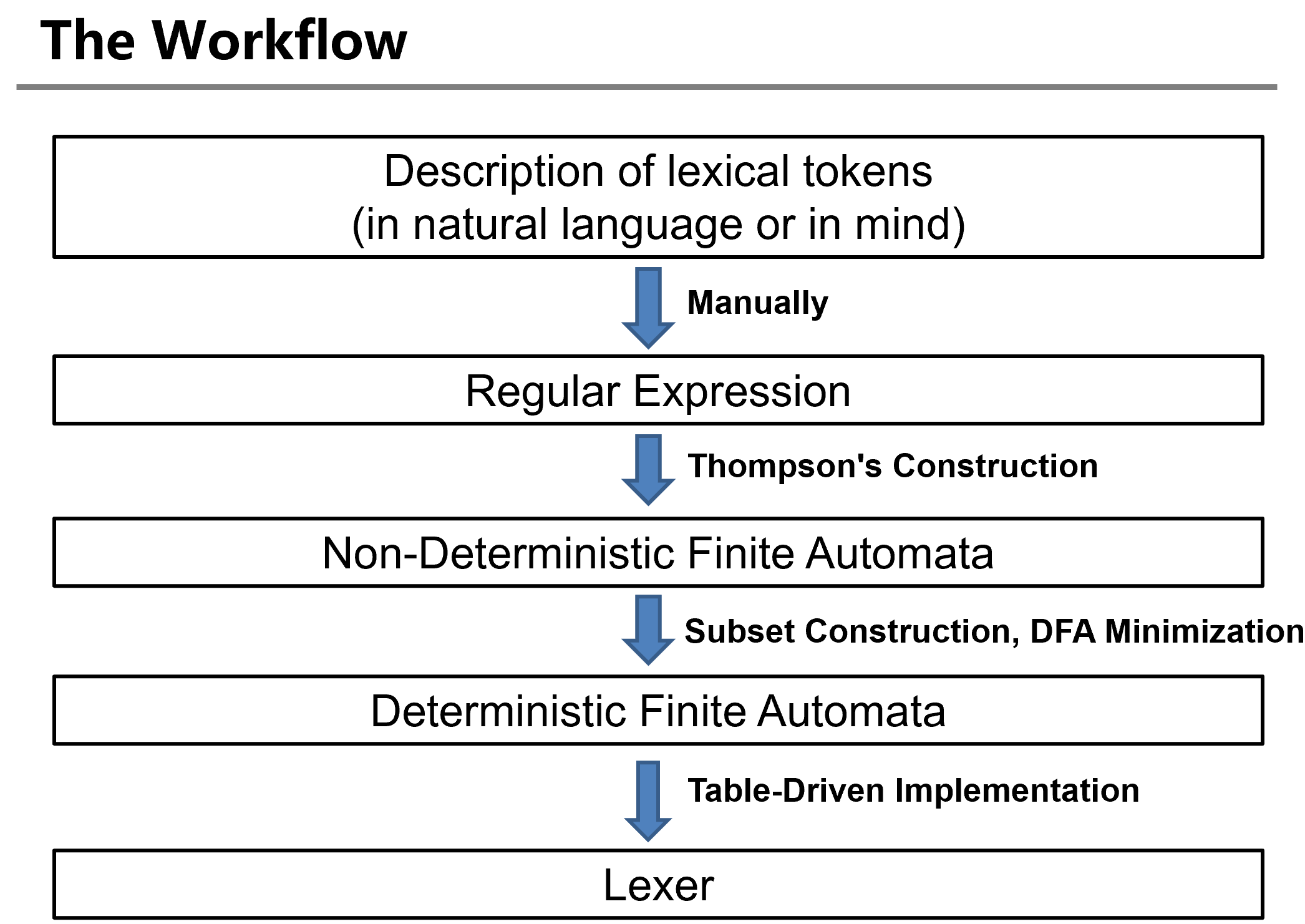
Lexical Token
定义:一个字母序列,文法中的基本单元。
常见的 token 有:

多数语言中保留词不作为 identifiers。
常见的 non-token 有:
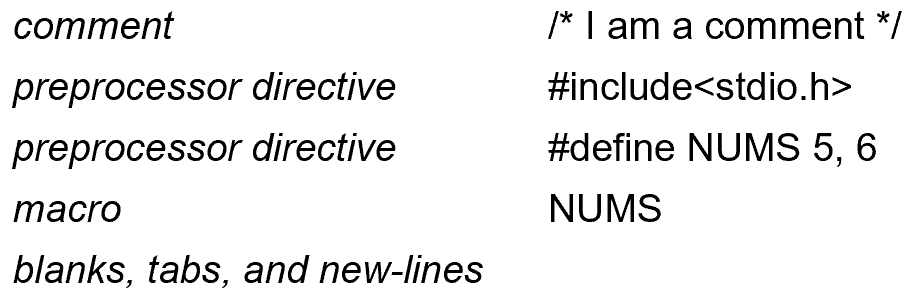
词法分析的示例如下:
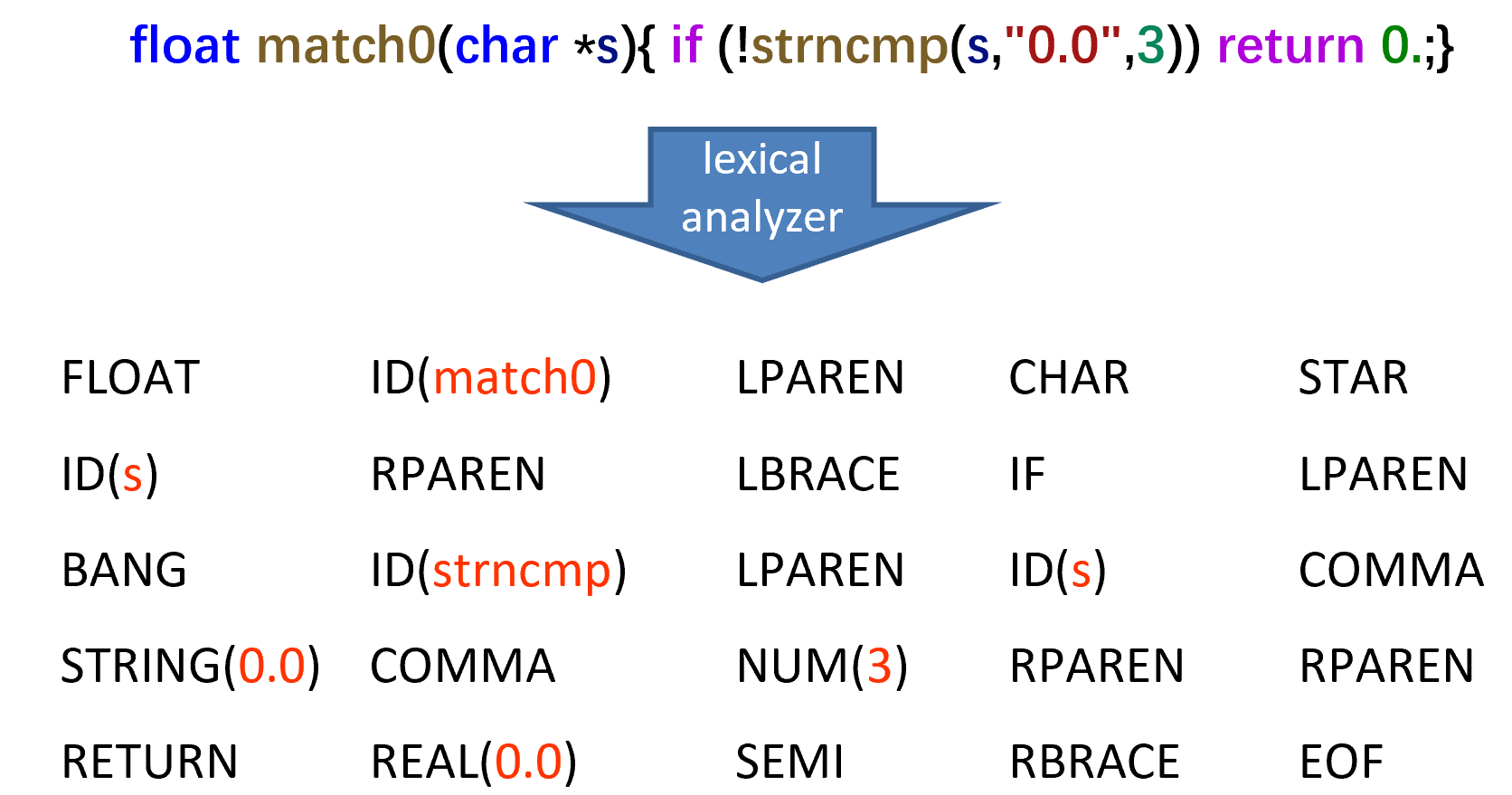
Regular Expression
使用正则表达式来描述 token 规则,再使用 DFA 实现上述的正则表达式。
词法分析阶段不用关心 string 的含义,只需要关心字符串是否在语言中。

Note
其中 a | \(\epsilon\)与 a | 等价。
Note
更多的简写:

简写不会让正则表达式的表达能力增加。
Note
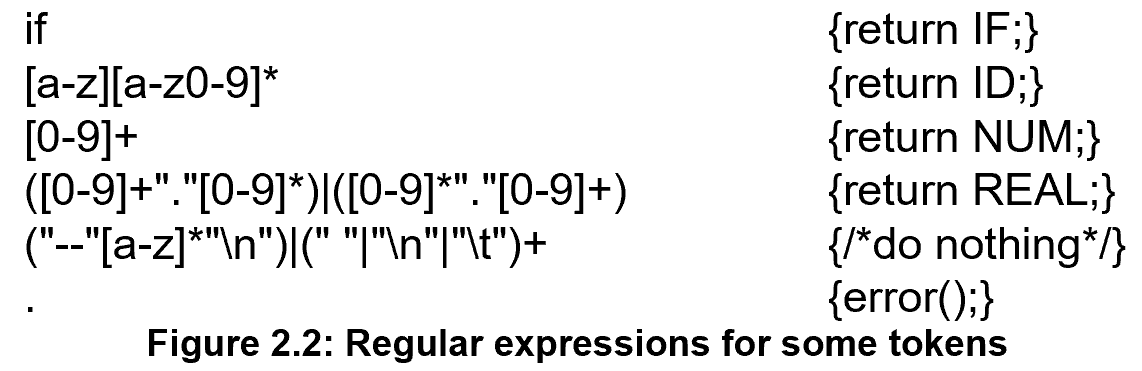
第五行表示的是注释或空格、换行等。
Warning
上述的例子中存在歧义,例如 if8 可以解释为 ID 也可以解释为 if + 8。
现代的编译器会引入最长匹配机制且按照规则的优先级逐条匹配 (if8 解释为 ID)。
Finite Automata
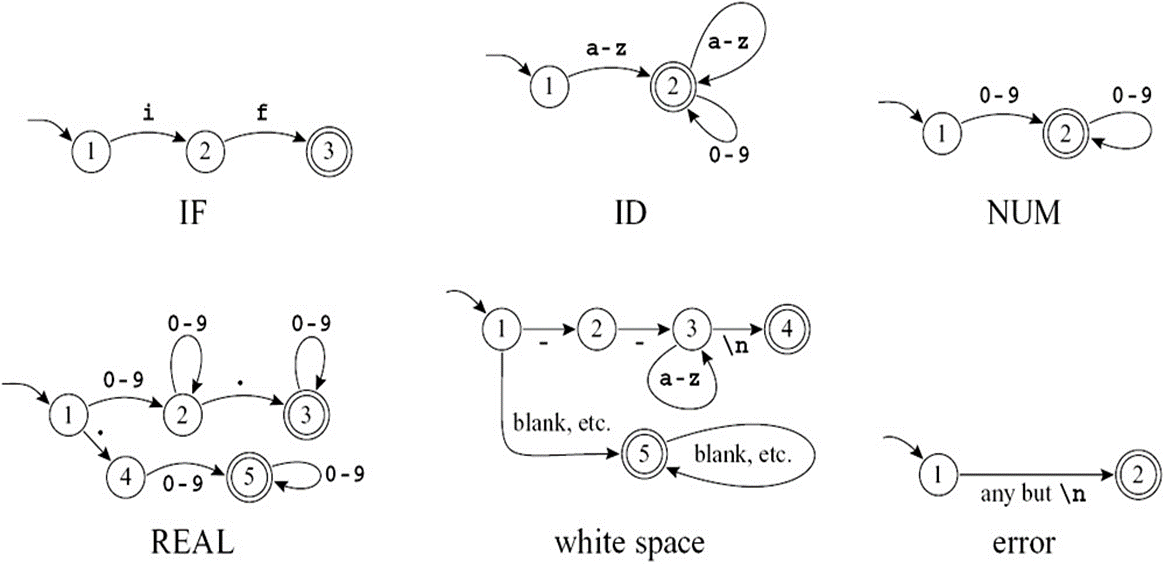
确定性状态机:no two edges leaving from the same state are labeled with the same symbol.
将上述的六个 DFA 拼接成一个 DFA:
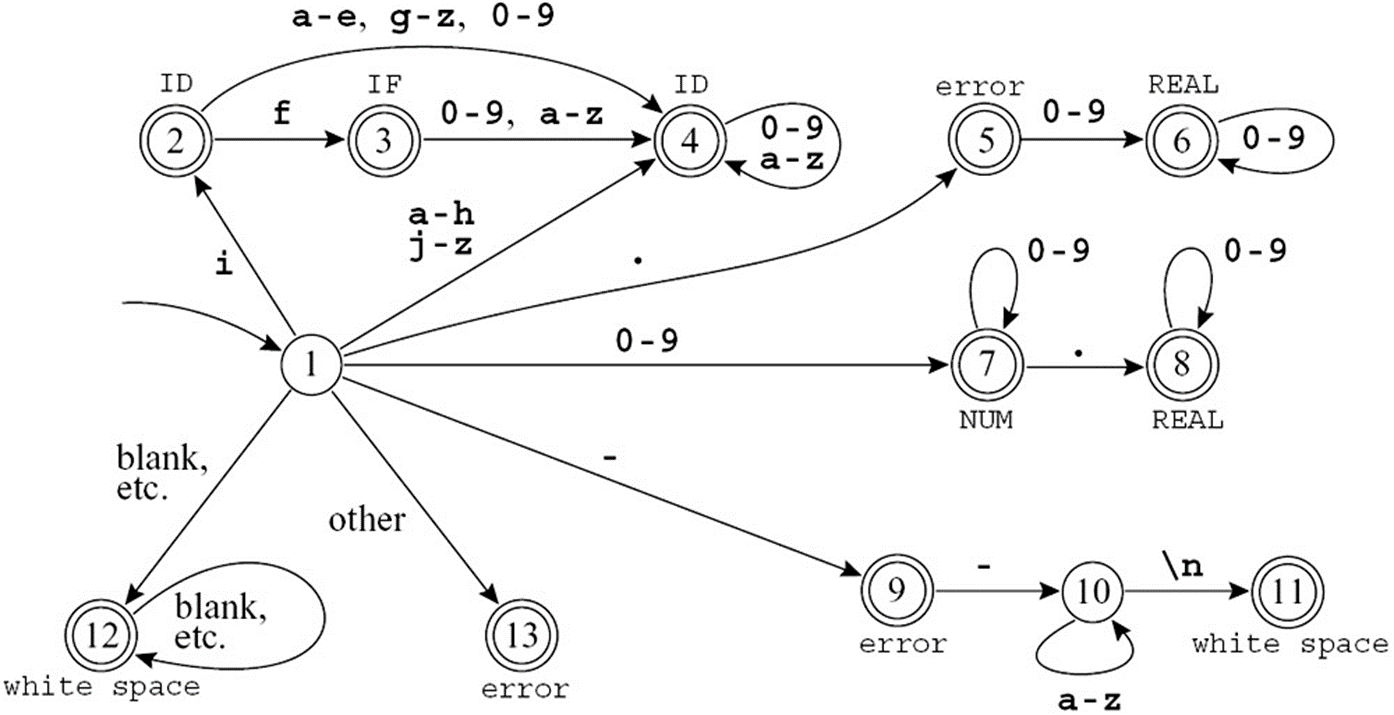
计算机中 DFA 的实际上通过表格的方式 ( transition matrix ) 实现的。
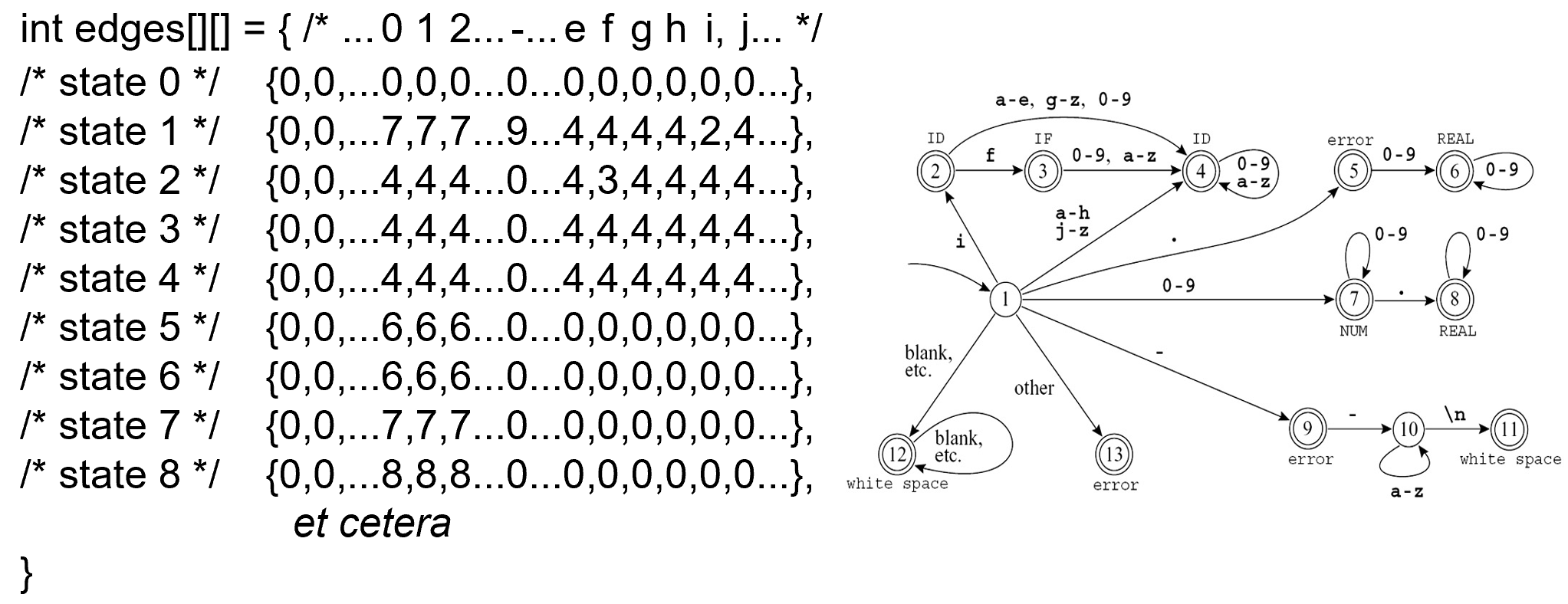
- 每一行表示一个状态,每一列表示读入的 symbol,存储的值表示读入后跳转到的状态。
- 0 表示错误状态。
额外需要一个矩阵存储每一个状态是否为终态 ( "finality" array ),以及其对应的输出标签是什么。
- 为实现 Longest matching,每次遇到可以终止的节点时,先记录当前的分析结果,继续向后扫描,直到无法扫描为止。
- 需要
Last-Final,Input-Position-at-Last-Final两个变量进行记录。 
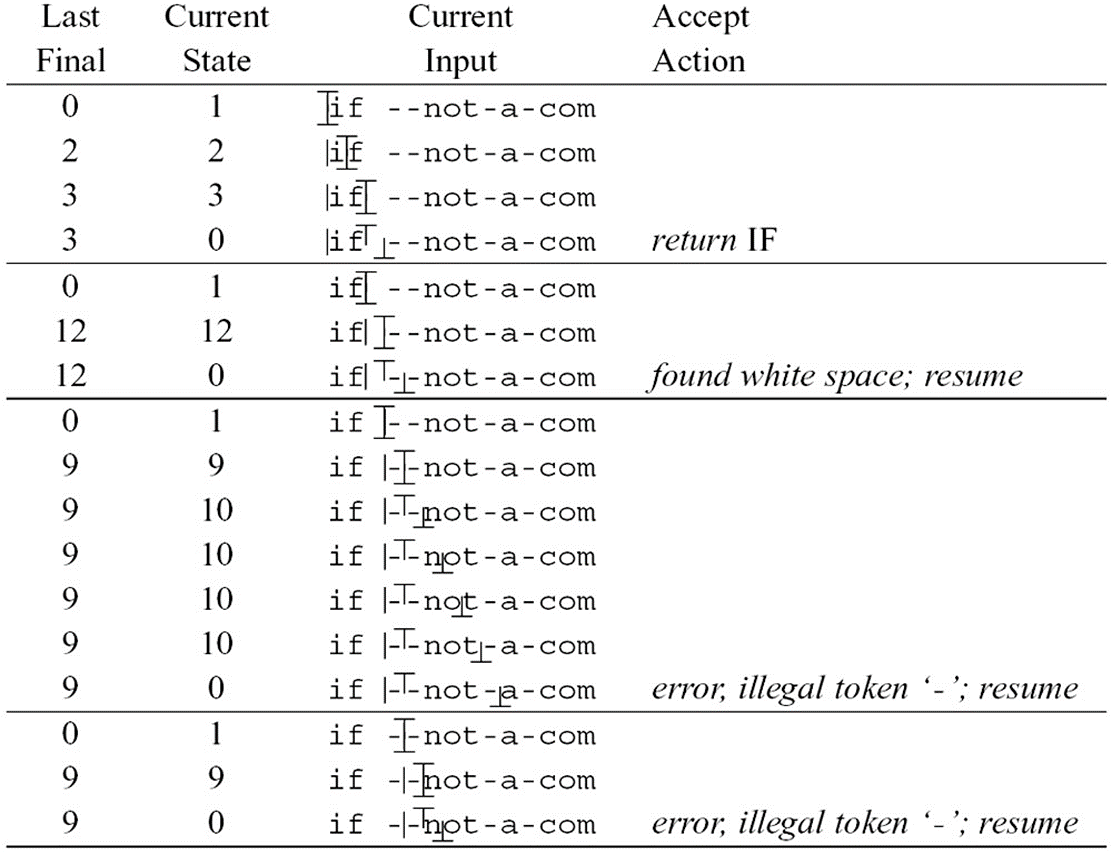
Nondeterministic Finite Automata
Thompson's Construction
将正则表达式转化为 NFA
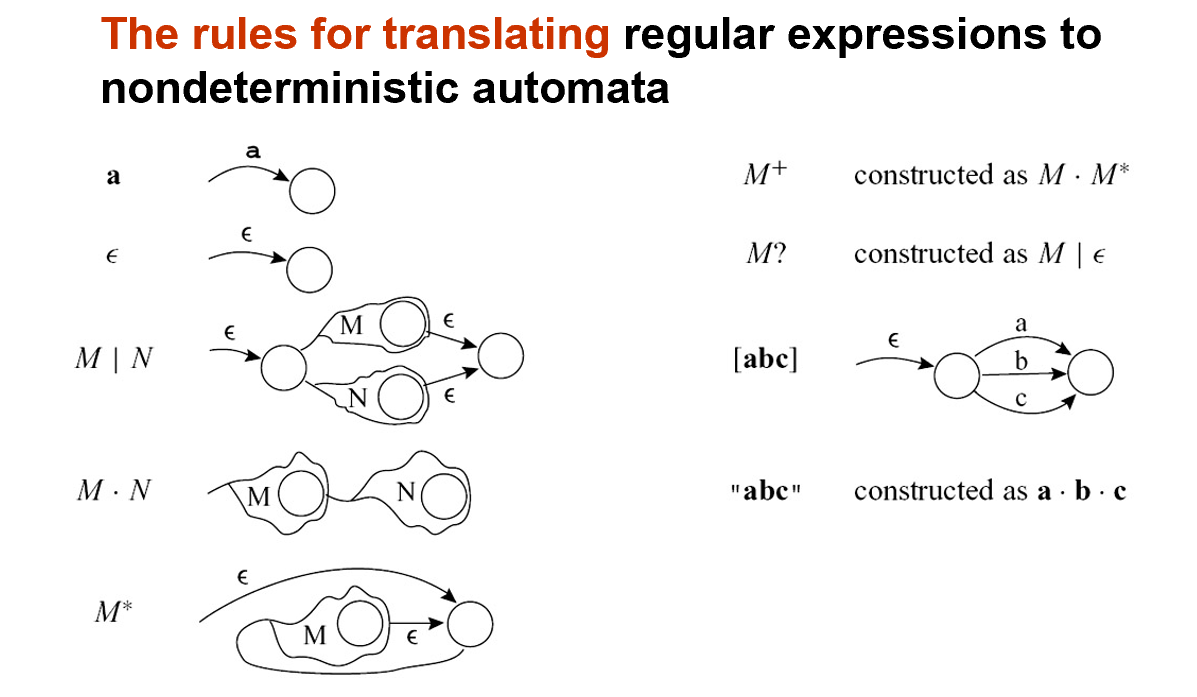
| Regular Exp | NFA |
|---|---|
 |
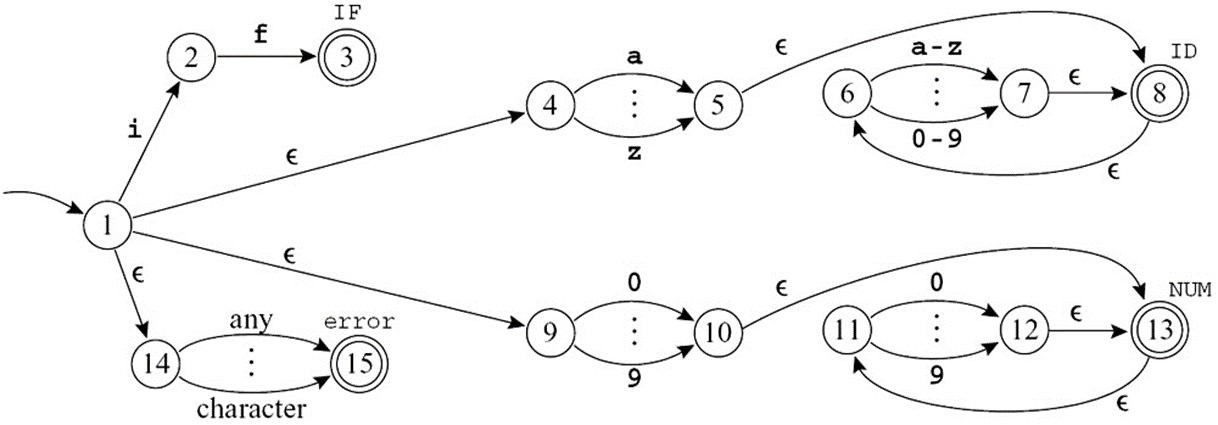 |
Subset Construction
将 NFA 转化为 DFA
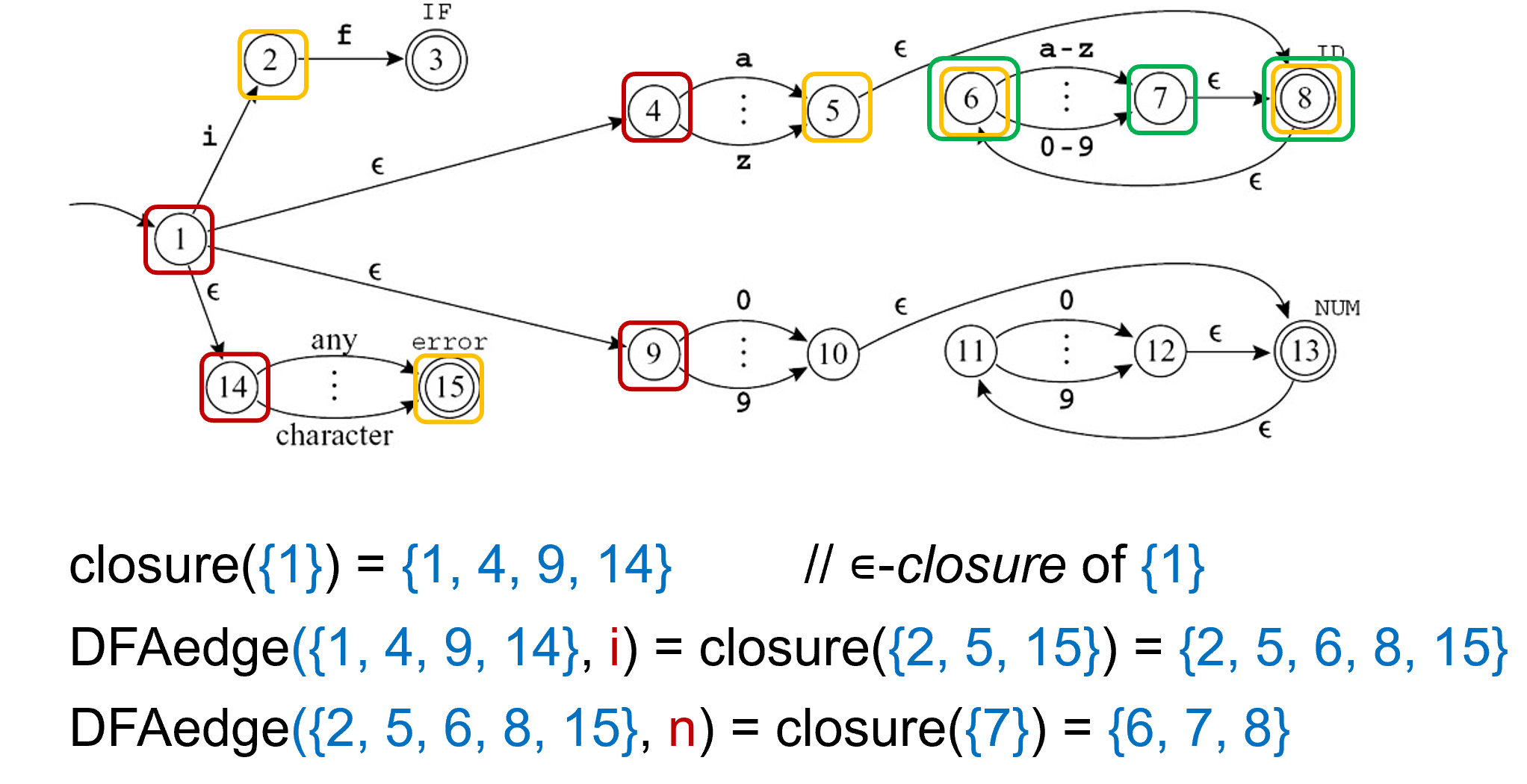
- edge(s, c):1.the set of all NFA states reachable by following a single edge with label c from state s.
- closure(S):the set of states that can be reached from a state in S without consuming any of the input, that is, by going only through ∊-edges.

算法思想:

算法实现:

算法例子:
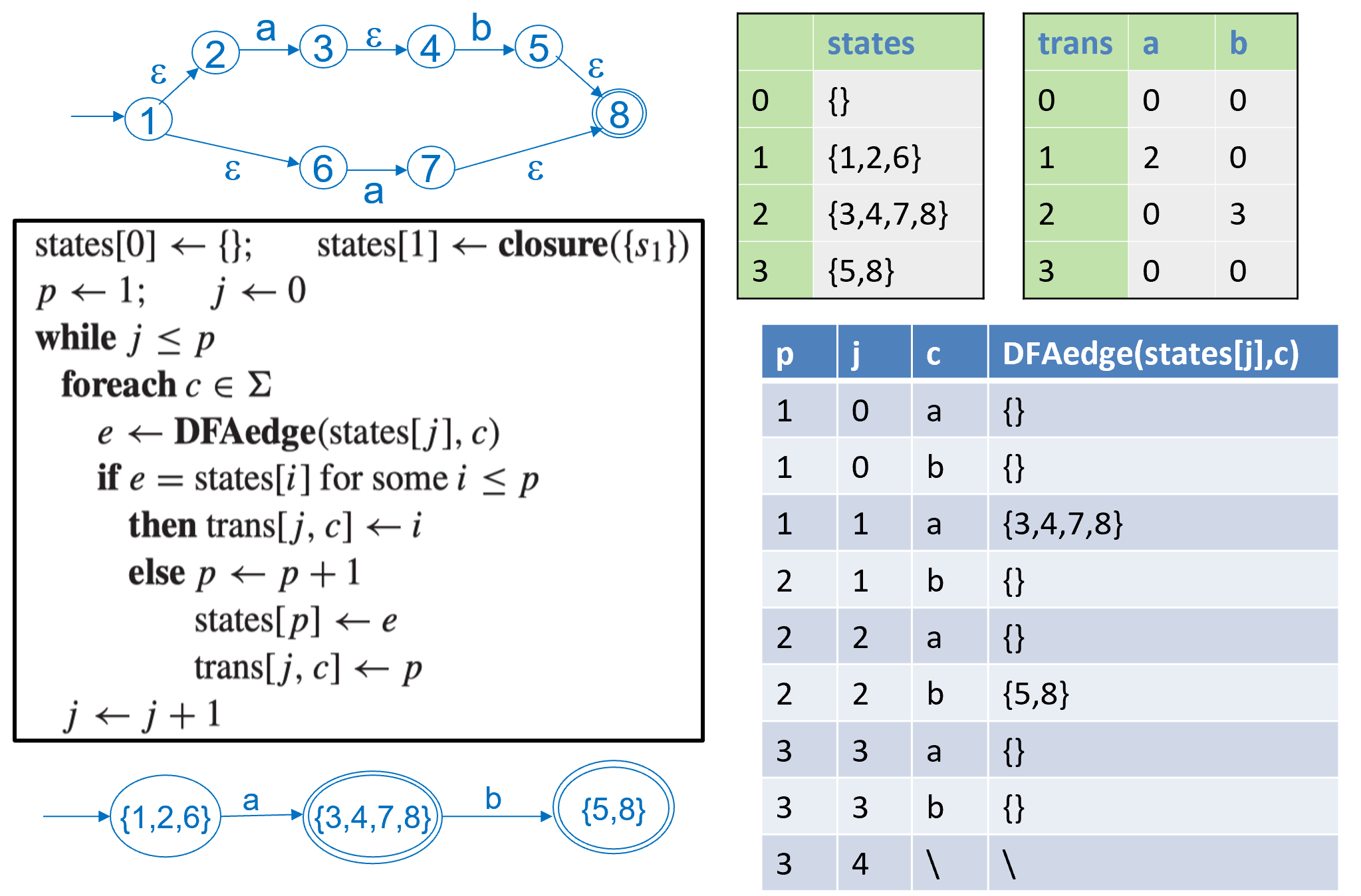
| NFA | DFA |
|---|---|
 |
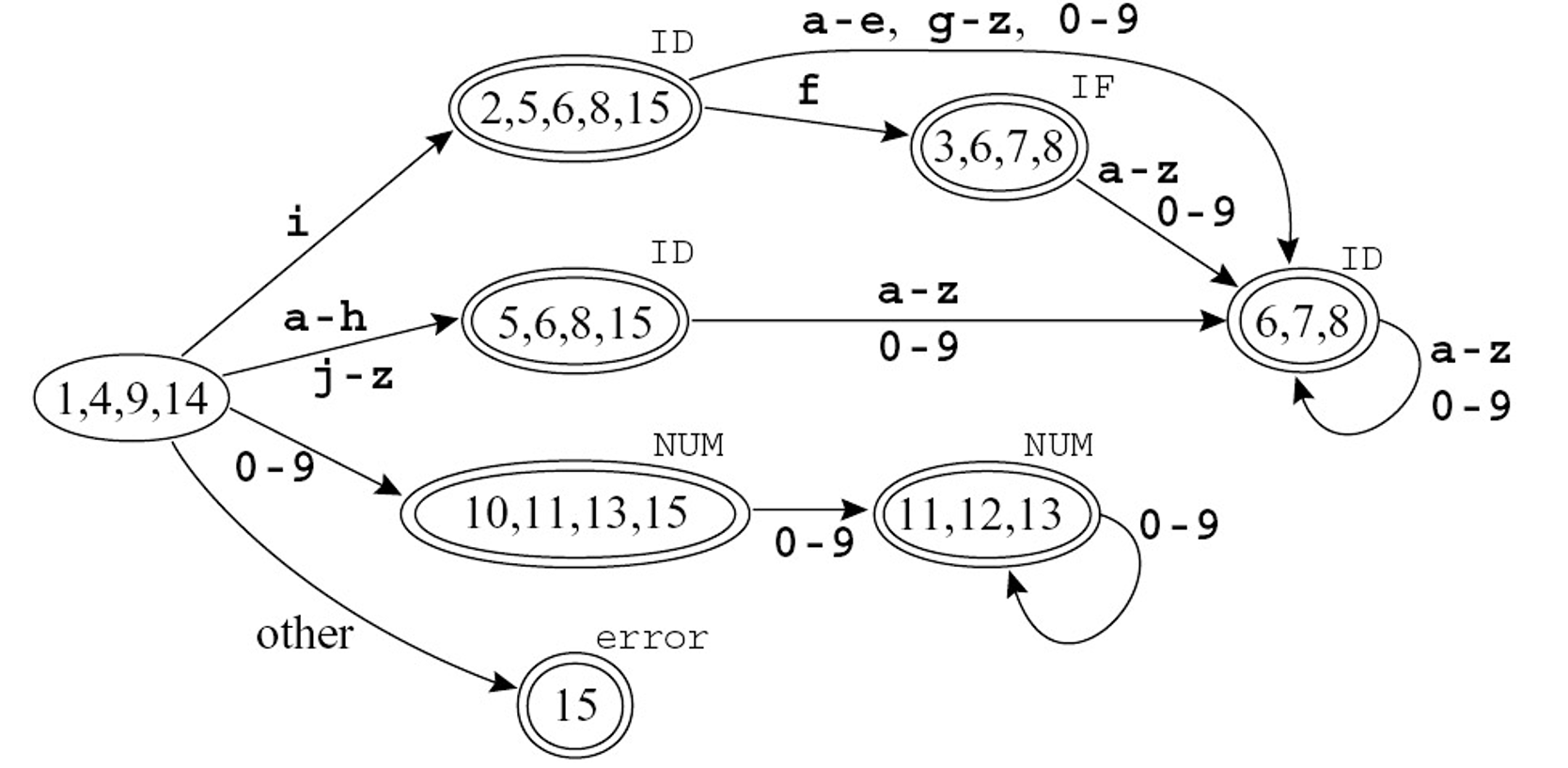 |
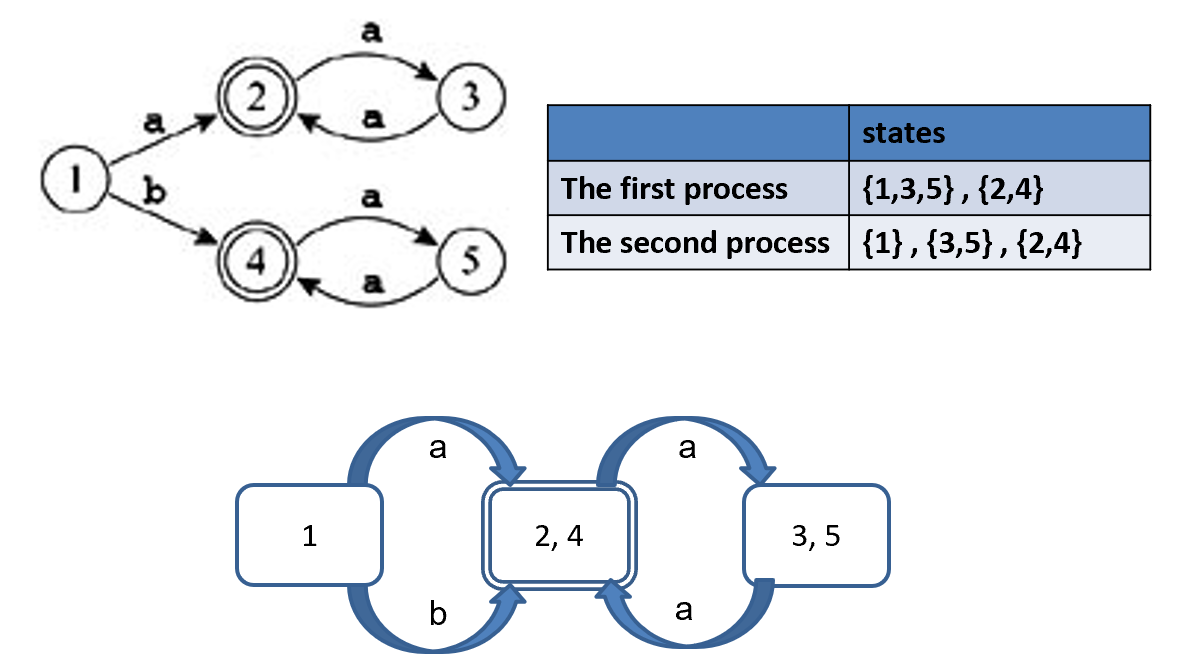
上述右图的部分等价状态可以合并,以缩小 DFA。但有部分的等价状态无法消除。

上述的算法总体思想为找到非等价的状态,举例如下:
Lex: A Lexical Analyzer Generator
Lex 是一个程序,
- 输入:a text file containing regular expressions, together with the actions to be taken when each expression is matched.

- 输出:Contains C source code defining a procedure yylex that is a table-driven implementation of a DFA corresponding to the regular expressions of the input file, and that operates like a getToken procedure.
Syntax analysis 语法分析
2024.03.14
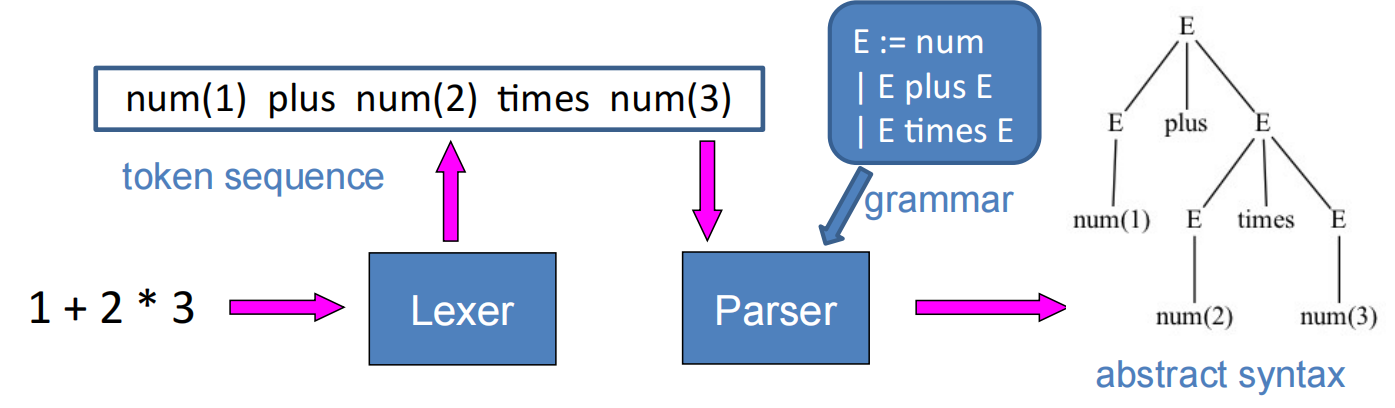
CFG 上下文无关文法
正则表达式的无法表达括号匹配等 Recursive Structure 规则。
CFG 在进行替换时不需要关心 non-terminal symbol 的左右 ( 上下文 ) 如何,根据规则进行替换即可。
一个不含分支语句的程序的 CFG 可以表达如下:

其中 S 表示语句,可以使用分号顺序连接。E 为数字或变量。
在判断程序是否正确时,主要思路为判断程序是否有语法错误。

上述推导遵循了最左推导 left-most derivation,可以根据次生成 parsing tree。某些情况下最左和最右推导等价 ( 当文法没有歧义时 )。
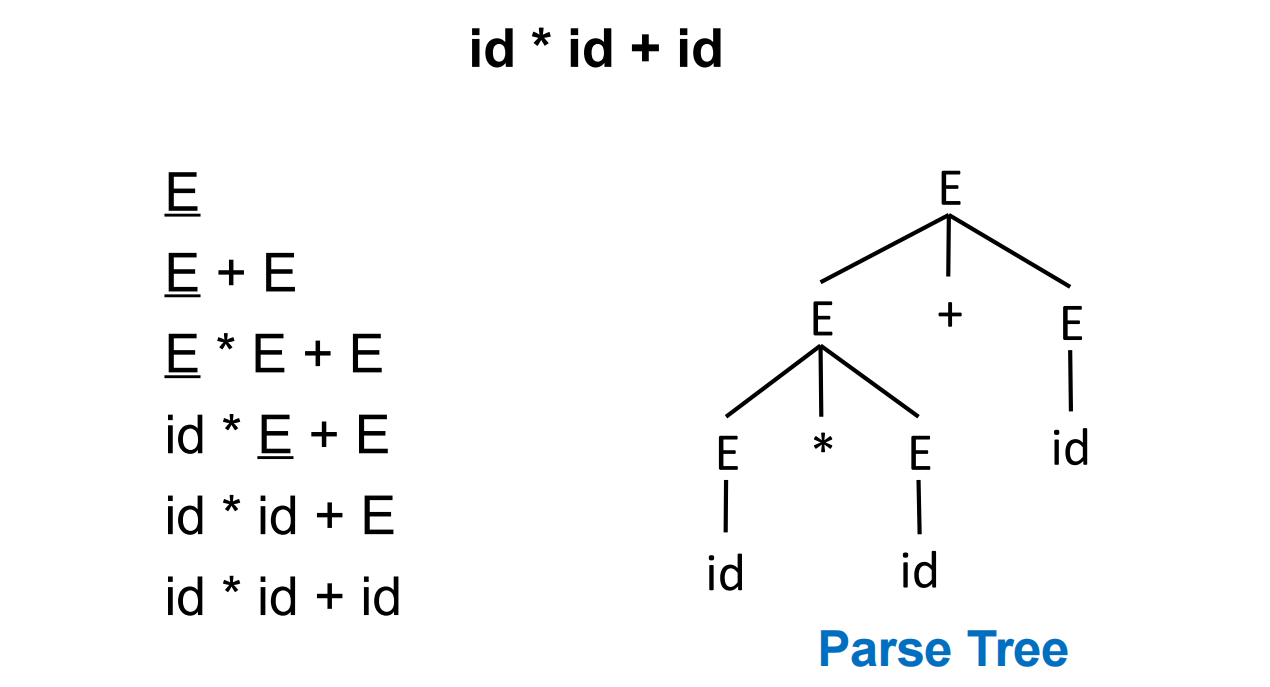
一颗 parsing tree 可能对应多个推导关系。
歧义
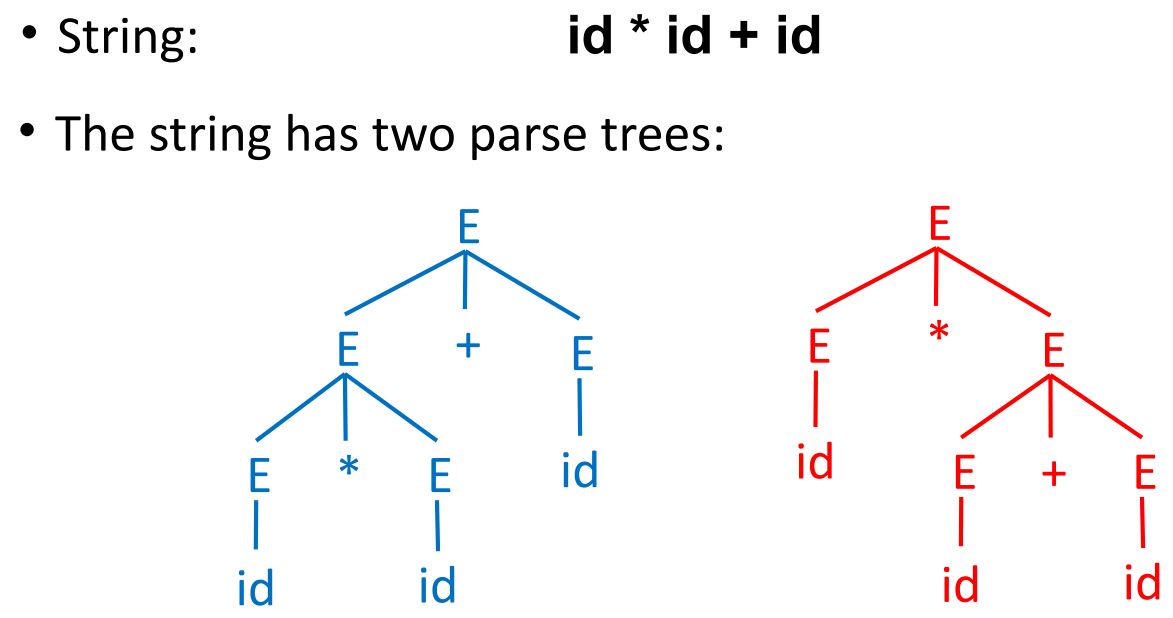
需要对生成的规则进行更改以消除歧义。规定乘法优先级高于加法,并统一进行左结合。

为识别是否已经读到文件的末尾,引入 $ (EOF)。在规则中加入 $S\rightarrow E $ $。
Top-Down Parsing
Recursive Descent Parsing: parses LL(1) grammars : Left-to-right parse; Leftmost-derivation; 1symbol lookahead.
根据读取到的 token,从左到右读取,尝试寻找规则进行匹配进行 parsing tree 的构建。

| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
上述的实现主要依靠替换后的第一个 symbol 进行规则的选择,但并不适用与所有的语法。
Predictive Parsing
对于无法通过第一个 symbol 进行判断 ( 例如都是 non-terminal),基于一定的规则进行计算首先派生出的 terminal symbol,再进行判断。
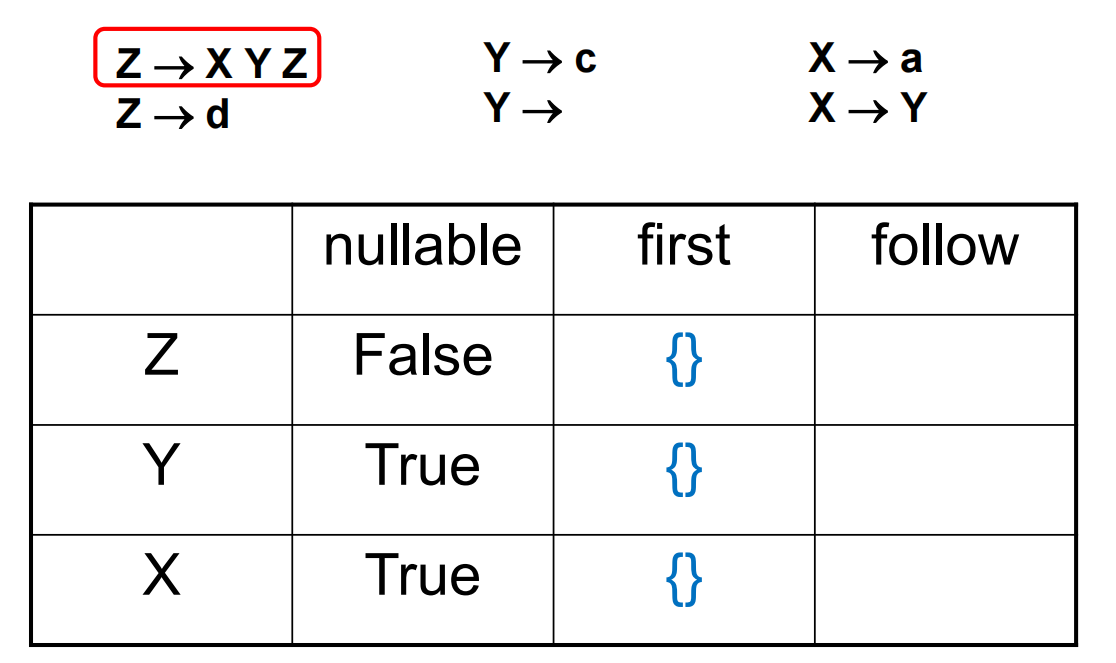
对于例如 \(Z\rightarrow XY\) 的规则,首先需要考虑的是 X 在派生之后会产生的第一个 terminal 符号 (First)。但需要考虑到 X 可能派生出空串\(\varepsilon\) (Nullable),所以需要考虑 Y 可能派生出的第一个 terminal。但 Y 若也可能派生出\(\varepsilon\) , 则需要考虑紧跟在 Y 之后的 terminal (Follow)。
\(\gamma\rightarrow^* t\beta\),其中 t 为 terminal symbol。\(\gamma\) 和 \(\beta\) 表示任意的字符串,\(t\in First(\gamma)\)。
\(X \rightarrow^* \alpha Xt \beta\),\(\alpha\) 和 \(\beta\) 表示任意的字符串,\(t\in Follow(X)\)。
计算 Nullable 算法:
| C | |
|---|---|
1 2 3 4 5 6 7 | |
需要注意的是,每一轮都需要遍历所有的规则,每一轮循环结束都需要和前一次的结果进行比较,直到没有变化后结束循环。

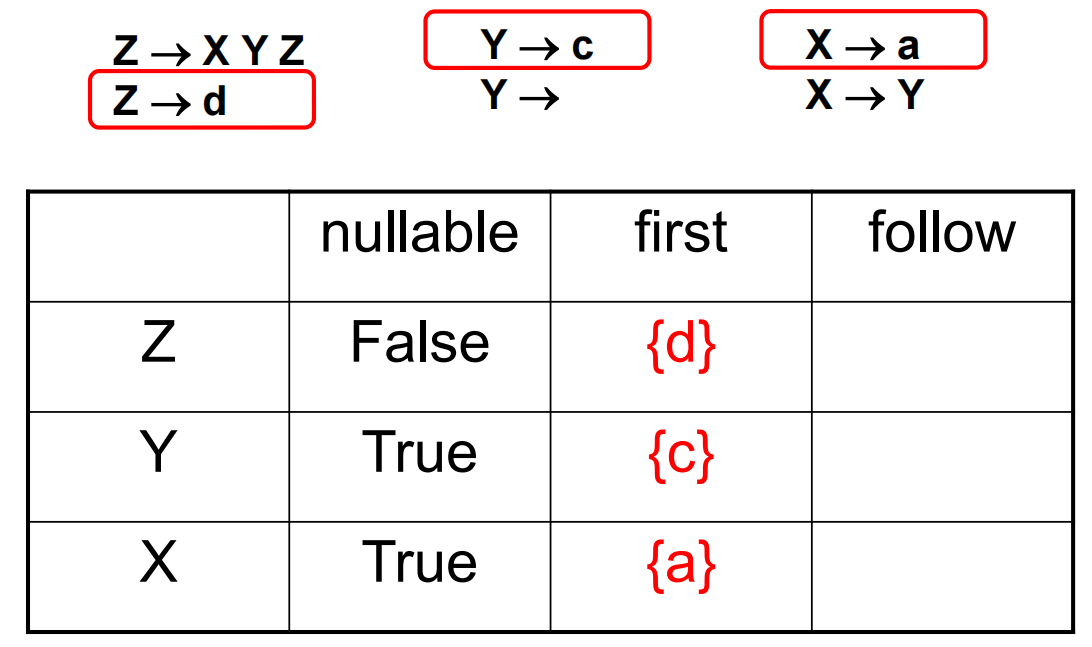
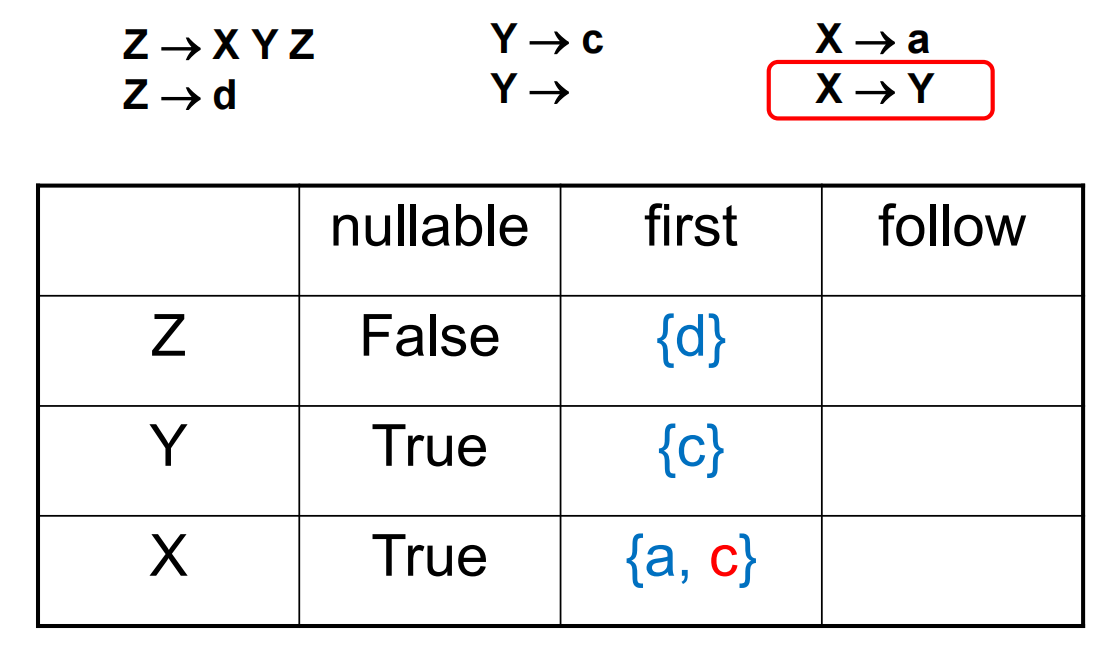
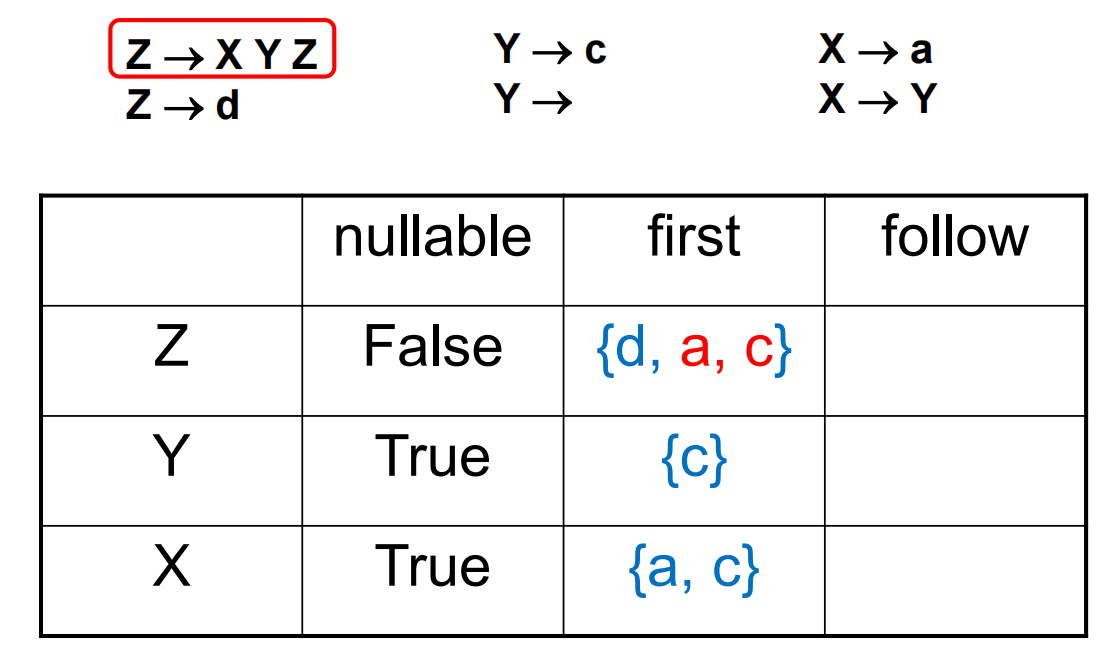
First 和 Follow 的算法如下:

举例如下:
| First-1 | First-2 | First-3 | First-4 |
|---|---|---|---|
 |
 |
 |
 |
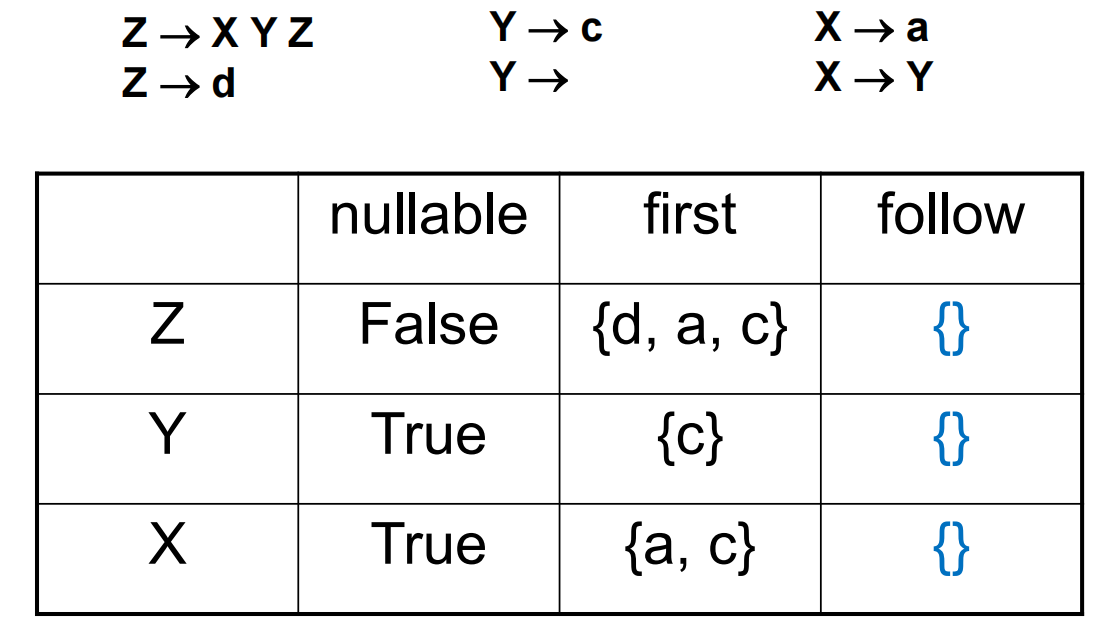
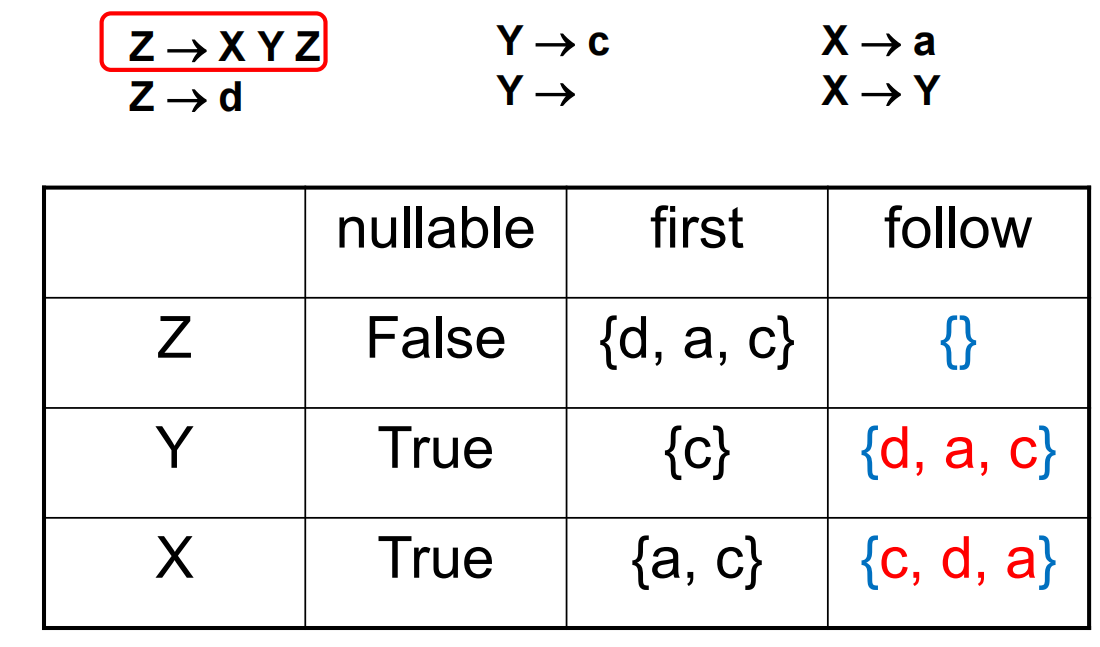
| Follow-1 | Follow-2 | Follow-3 |
|---|---|---|
 |
 |
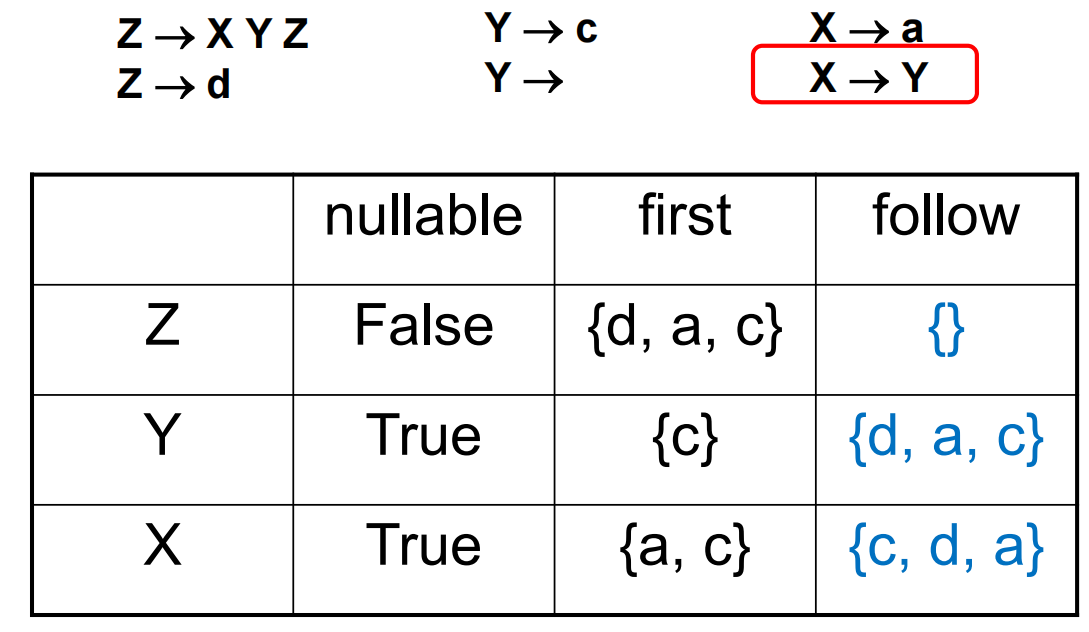 |
需要额外注意的是 \(X\rightarrow Y\) 规则会使 Follow(Y) 和 Follow(X) 出现重合。最终可以得到如下表格:
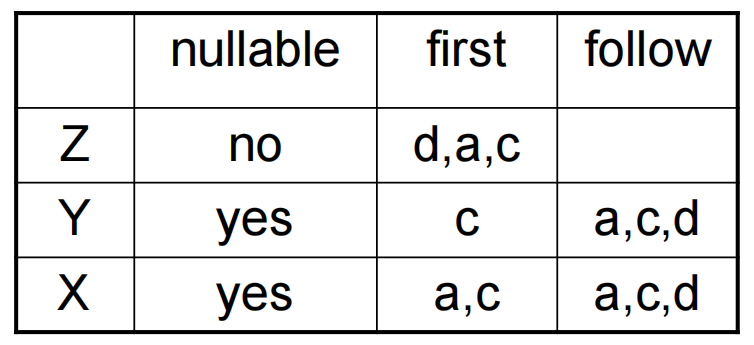
需要将上述的表格转化为一下的表格,以指明使用那条规则进行 parsing tree 的构建:
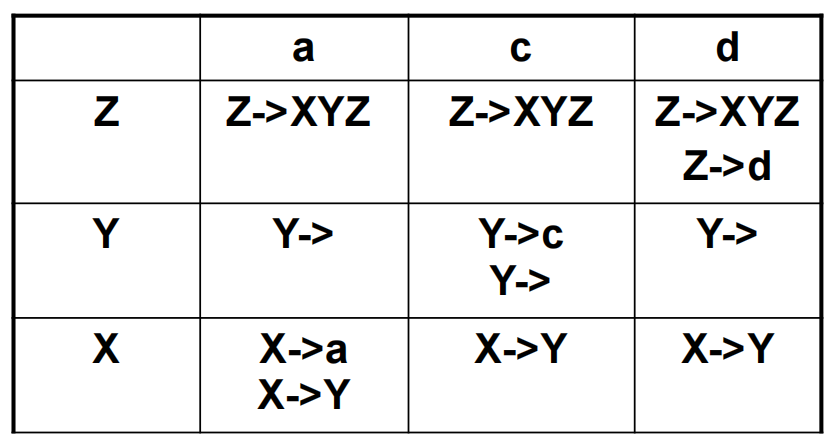
构建的算法如下:
- if T \(\in\) First(\(\gamma\)) then enter \(X\rightarrow \gamma\) in row X, col T.
- if \(\gamma\) is Nullable and T \(\in\) Follow(X) then enter \(X\rightarrow \gamma\) in row X, col T.
上述的表格指的是,在自顶向下派生 non-terminal 时,读到词法分析得到的序列中的某个 symbol 时需要选择的规则。若是查表得到了空格,则表示出现了语法错误。
还需要注意上述的表格还存在多条规则一个空格的情况,这可能由两种情况导致:
- Left-Recursive:\(A\rightarrow A\alpha,\,A\rightarrow\beta\).
- 修改后:\(A\rightarrow\beta A',\,A'\rightarrow\alpha A', A'\rightarrow \varepsilon\).
- Left-Left Factoring:修改如下:
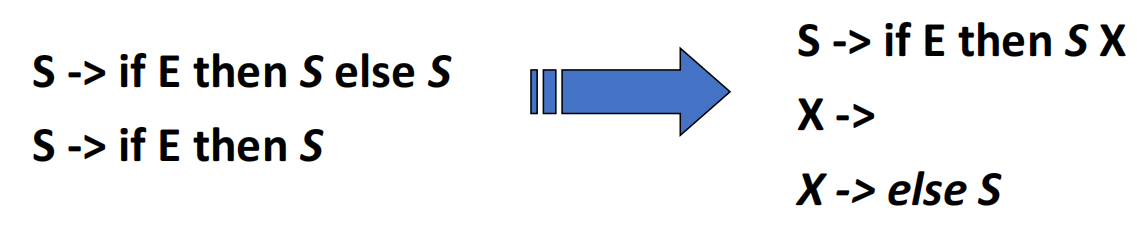
举例如下:

错误恢复
一般来说,在遇到错误后,需要从错误中恢复过来继续进行语法分析,以分析得到更多的潜在的语法错误。
常见的做法如下:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 | |
LL(k)
k 表示在选择派生规则时需要根据几个 input 才能判定。LL(1) 就表示一个 1 个 token 就能无歧义的进行规则选择。
every LL(k) grammar is an LL(k+n) grammar, for any n.
所以在例如在证明一个 grammar 是 LL(3) 时,可以先尝试证明其为 LL(1).
LR(k) parsing
相比 LL(k),不急于做匹配,直到 input tokens corresponding to the entire right-hand side of the production.
- 特征:Left-to-right parse、Rightmost derivation、k-token lookahead。
- 是一种
bottom-up Parsing。 - 不断将产生式的右部替换为左部。
举例如下:
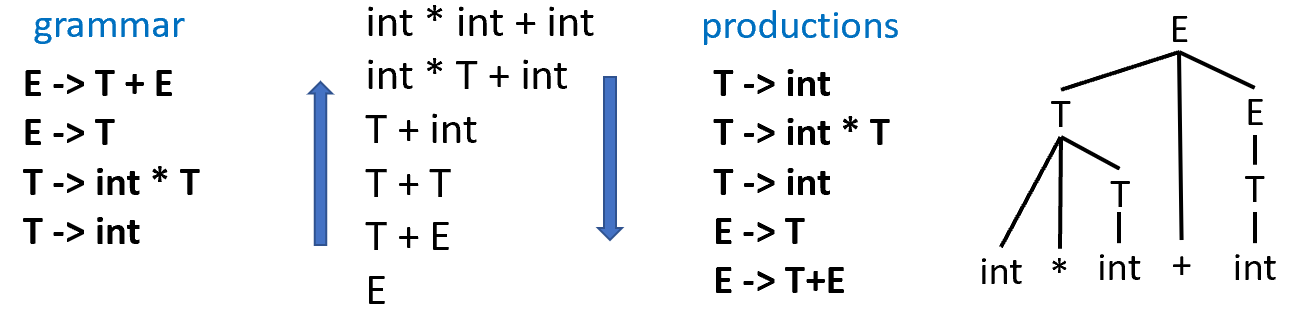
从以上的过程可以看出以上的过程自下往上看实际上为最右展开。

分为 shift 和 reduce 两个过程。
-
shift: push next input onto top of stack
-
reduce R:
- top of stack should match RHS of rule R (e.g., X -> A B C)
- pop the RHS from the top of stack (e.g., pop C B A)
-
push the LHS onto the stack (e.g., push X)
-
error
-
accept: shift $ and can reduce what remains on stack
LR(0) Parsing
只需要在 state stack 中看就可以判断。
可以使用 DFA 来确定是否 reduce。
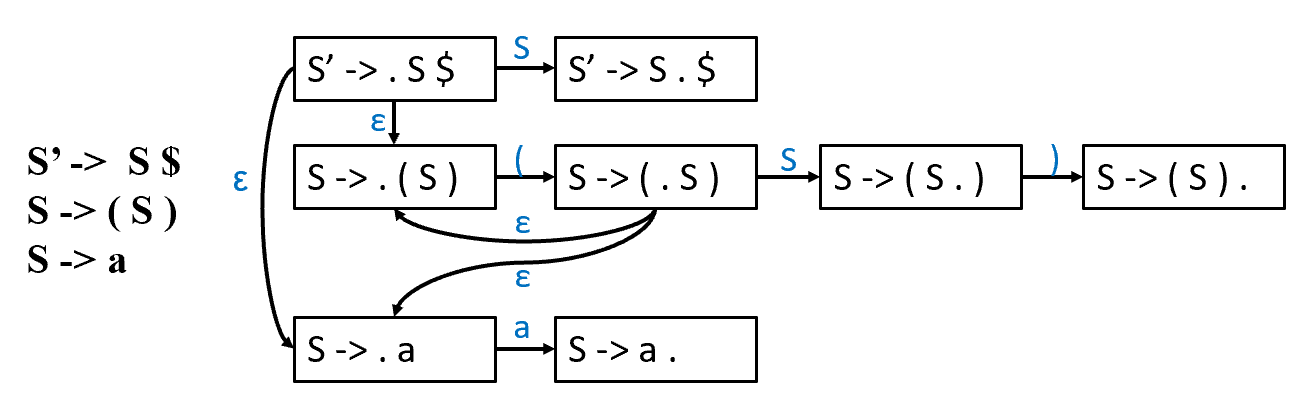
-
. : the current position of the parser
-
start with S’ -> . S $: stack should be empty and the input is expected to be a complete S-sentence followed by $
- A -> 𝛼 . β: LR(0) item
- means the parser has processed 𝛼 and expects to see β next.
接下来将 NFA 转化为 DFA。
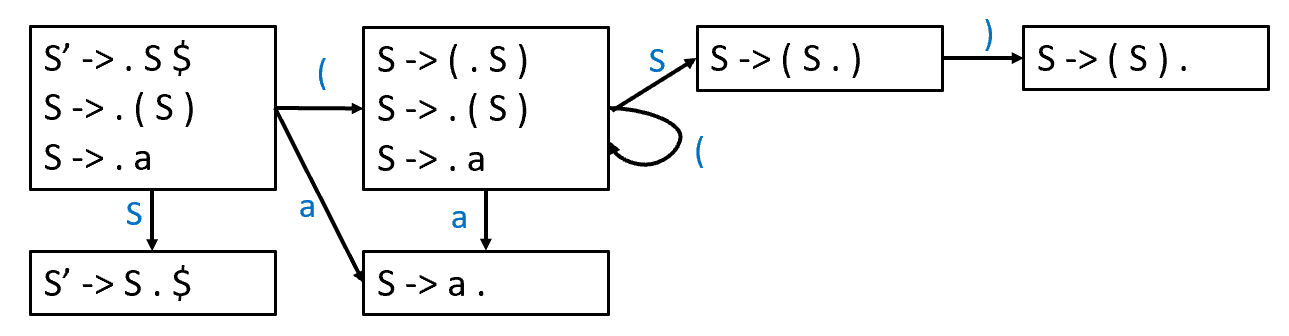
具体算法如下:

应用上述的算法,对于 grammar:
S’ -> S$ S -> ( L ) S -> x L -> S L -> L , S
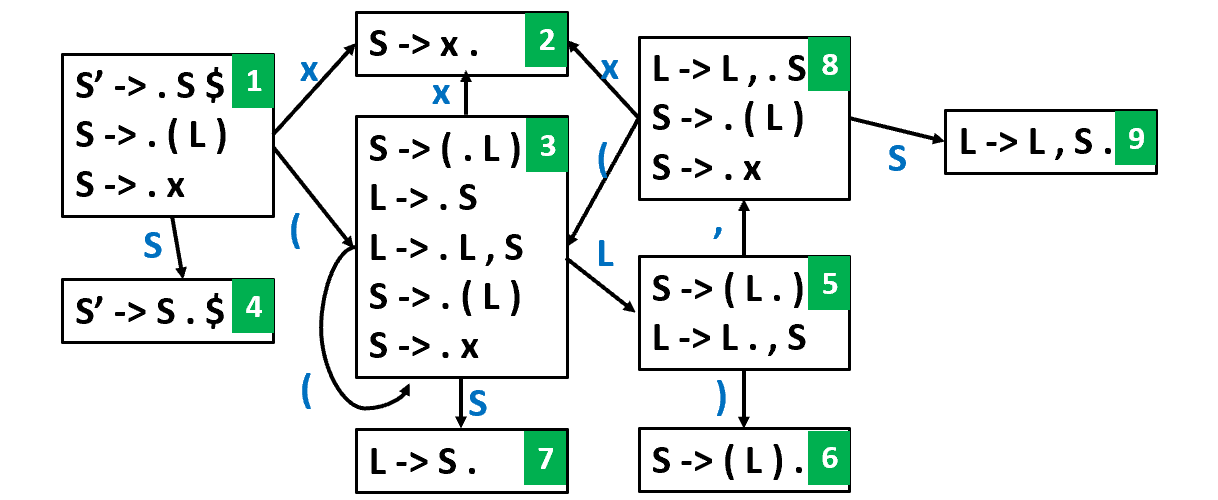
| Stack (states) | Stack (symbols) | Input | Action |
|---|---|---|---|
| 1 | ( x ) $ | shift 3 | |
| 1, 3 | ( | x ) $ | shift 2 |
| 1, 3, 2 | ( x | ) $ | reduce 2 S -> x |
| 1, 3 | ( S | ) $ | goto 7 |
| 1, 3, 7 | ( S | ) $ | reduce 3 L -> S |
| 1, 3 | ( L | ) $ | goto 5 |
| 1, 3, 5 | ( L | ) $ | shift 6 |
| 1, 3, 5, 6 | ( L ) | $ | reduce 1 S -> ( L ) |
| 1 | S | $ | goto 4 |
| 1, 4 | S | $ | accept |
可以得到以下的 parsing table:
| ( | ) | x | , | $ | S | L | |
|---|---|---|---|---|---|---|---|
| 1 | s3 | s2 | g4 | ||||
| 2 | r2 | r2 | r2 | r2 | r2 | ||
| 3 | s3 | s2 | g7 | g5 | |||
| 4 | a | ||||||
| 5 | s6 | s8 | |||||
| 6 | r1 | r1 | r1 | r1 | r1 | ||
| 7 | r3 | r3 | r3 | r3 | r3 | ||
| 8 | s3 | s2 | g9 | ||||
| 9 | r4 | r4 | r4 | r4 | r4 |
具体的操作规则如下:
- Shift: For edge labeled with terminal t and from state i to state n:
-
T[i, t] = sn (shift n)
-
Goto: For edge labeled with non-terminal X and from state i to state n:
-
T[i, X] = gn (goto n)
-
Reduce: For item in a state i with dot at the end (e.g., X -> A … C .):
-
T[i, each terminal] = rk (reduce k)
-
k is the index of this production
-
Accept: For each state i containing
-
S’ -> S . $:
-
T[i, $] = accept
Simple LR Parsing
可能会存在 shift-reduce 冲突,即无法判断是否需要 reduce。
引入 SLR 方法,基本思想是计算 Follow 集合:
| C | |
|---|---|
1 2 3 4 5 6 7 8 | |
LR(1) Parsing
需要往后看一个 symbol 以辅助动作选择。
- ( \(A \rightarrow \alpha.\beta\), x), x 表示 \(\beta\) 处理完之后,将看到的 symbol。
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
Abstract Syntax 抽象语法
2024.04.11
如何构建抽象语法树 AST,如何将语义信息处理加入到加入到语法分析中去。
Note
在 recursive-descent parser 中,语义动作有 values ( 如算式结果 ),或者 side effects ( 如赋值语句、函数调用 ),都需要记录。

一些情况下需要进行语义值得传递。例如:T → F T′;T′ → *F T′;T′ → / F T′,需要将 F 的值向下传递。
Note
Yacc 中的部分语法:
{ … }: semantic actions
$i: the semantic values of the i_th RHS symbol
$$: the semantic value of the LHS nonterminal symbol
%union: difference possible types for semantic values to carry
<variant>: declares the type of each terminal or nonterminal
Yacc 代码举例如下:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
Abstract Syntax Tree
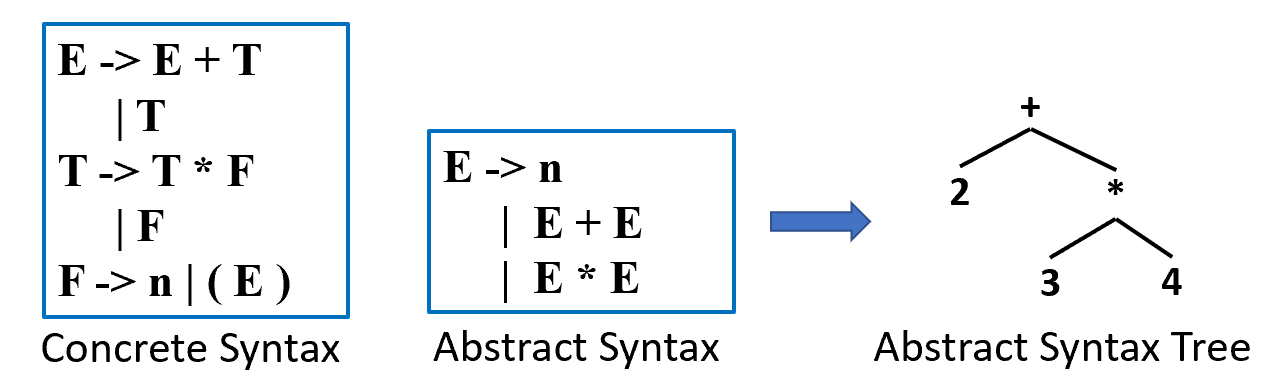
相比具体语法,抽象语法略去了一些冗余的信息便于计算机进行处理。
为方便错误恢复,可以记录下每一个 token 的位置信息。
Semantic Analysis 语义分析
2024.04.11
如何将声明与使用联系到一起,检查表达式是否正确。
Symbol Tables 符号表
environment:变量与其类型的定义绑定。- \(\sigma_0=\{g\rightarrow string, a\rightarrow int\}\)
- \(\sigma_1=\sigma_0+\{b\rightarrow string, a\rightarrow int\}\)
- 两个符号表存在一个“冲突”,需要注意到的是局部类型可以覆盖全局的类型。加号右侧的优先级更高。
- 一个局部语句块结束时,可以抛弃局部的符号表:
- discard \(\sigma_1\), go back to \(\sigma_0\)
实现符号表有两种方式:
- Functional Style:保留每一级的符号表。
- Imperative Style:只是在一个符号表上进行修改。
对于一些面向对象的语言,需要有多个符号表,例如:
| Java | |
|---|---|
1 2 3 | |
可以写作:\(\sigma_0 = \{a\rightarrow int\},\,\sigma_1=\{E\rightarrow \sigma_0\}\)
符号表在具体实现时经常使用哈希表以实现快速的插入与删除:
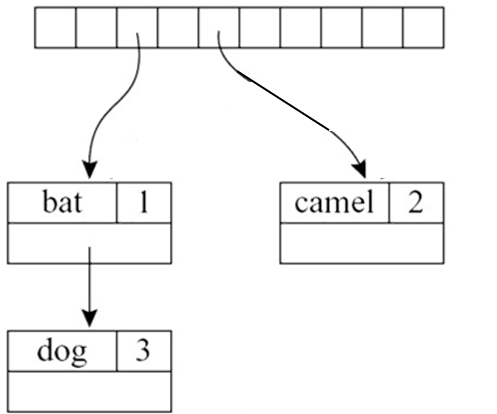
对于函数式的符号表,可以使用如下的指针方式高效实现:
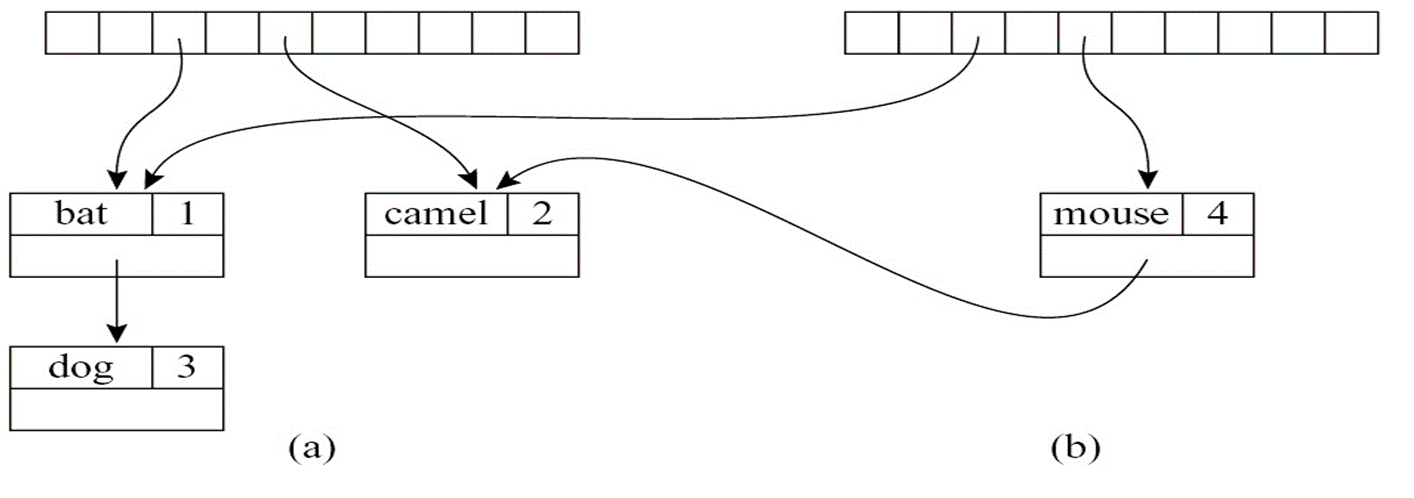
但若是符号表巨大,复制仍然需要较多的时间,可以使用二叉搜索树代替哈希表以加速复制的过程:
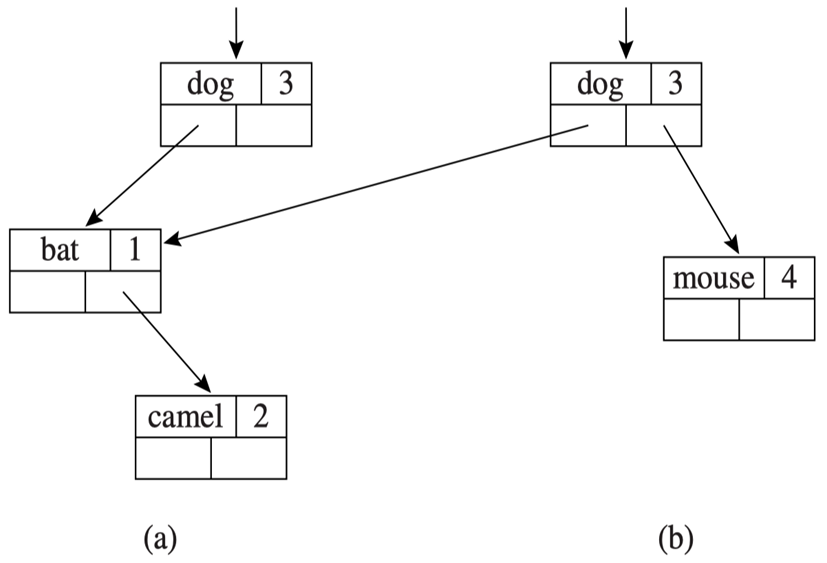
语义分析中不在乎字符串是否匹配,可以将字符串转化为 symbol 以加速 Hash 操作。symbol 可以直接作为 hash key,用于匹配,还可以在二叉搜索树中作为索引。
Tiger 语句中有两种绑定:类型绑定 (Typedef)、变量绑定
Type-checking 类型检查
实际上是对于 AST 的一个递归遍历的过程。
需要考虑的情况有:
-
检查赋值的类型是否一致。
-
将函数名与其参数表一块放进 environment。
-
结构体中存在大量的递归定义:
| C | |
|---|---|
1 2 3 4 | |
如果直接进行检查会出现死锁的情况,此时先检查结构体,使用占位符 ( 如:Ty_Name) 先代替类型。最后进行处理。
但如果存在下述的循环定义情况则不可:
| C | |
|---|---|
1 2 3 4 5 6 7 8 | |
会出现环,无法获取具体的类型。但下述的情况可以:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 | |
类型检查也需要检查环的情况。
- 对于循环函数递归调用:
| C | |
|---|---|
1 2 3 4 5 6 | |
只需要先计算出一者的返回值和类型、参数表等即可。
Activation Records 活动记录
2024.04.18
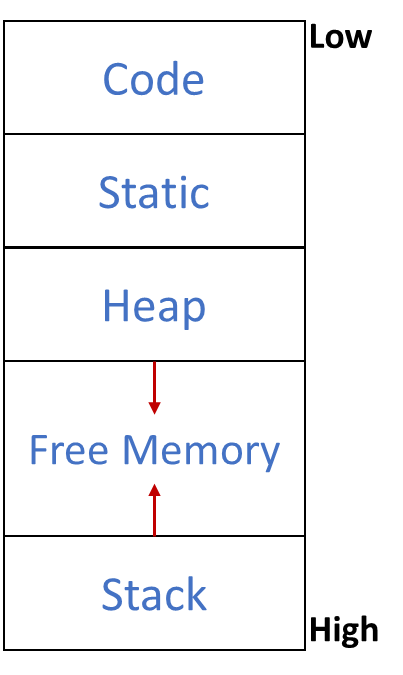
此章节主要关心 stack:data structures called activation records that get generated during procedure (i.e. function) calls.
-
Procedure (i.e., function) calls and returns are usually managed by a run-time stack called control stack.
-
Each time a procedure is called, space for its local variables is pushed onto the stack.
-
When the procedure terminates, that space is popped off the stack.
-
Procedure calls are also called activations of procedures.
-
Each live activation has an activation record (sometimes called a frame) on the control stack.
但若可以同时出现 nested function 和 functio-valued variables (e.g. 函数指针 ),栈这种类型的数据结构就不够用了。
| JavaScript | |
|---|---|
1 2 3 4 5 6 7 8 9 10 | |
Stack frame
Local variables are pushed/popped in large batches
Local variables are not always initialized right after their creation
We want to continue accessing variables deep within the stack
所以需要将栈视为数组,可以访问非栈顶的元素。
此外还维护了一个 Stack pointer。
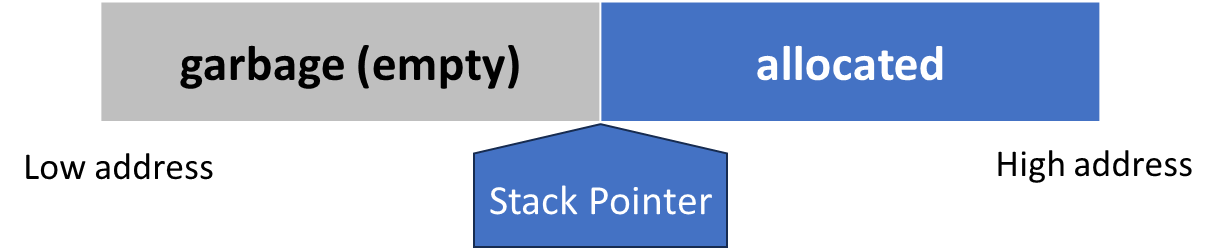
具体的设计如下:
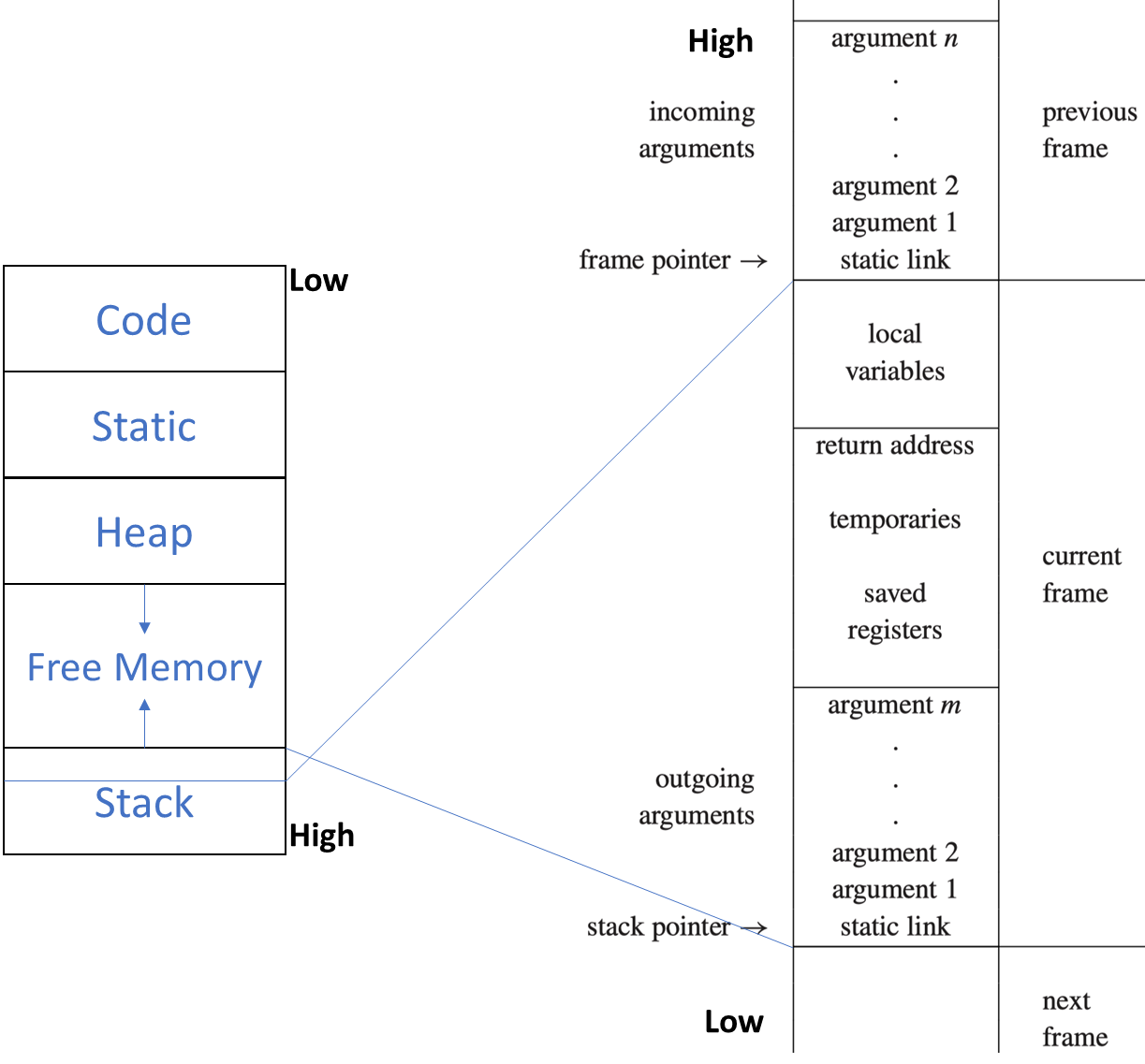
其中 previous frame 为 caller 函数,current frame 为 callee 函数。
incoming arguments: passed by the caller
outgoing arguments: pass parameters to other functions
可以看到参数是以倒序压在栈中的,这是为了提高指针查询的效率。
针对于之前提到的函数嵌套等问题,此处通过 static link 来进行栈帧与栈帧之间的连接。
可以看到除了栈指针外还维护了一个帧指针。在调用新函数时,会记录下老 FP 的位置,以便回退。
这种双指针的方式对于非连续内存排布或帧大小可变等情况会较为有效。
对于传参,由于寄存器的数量有限,一般情况下只有前 k 个参数通过寄存器进行传参,剩下的参数通过内存传递。但需要注意到由于使用了寄存器进行传参,需要将之前的寄存器都存进内存,似乎会拖慢性能。使用寄存器传参在以下的几个情况有效:
- Leaf procedures need not write their incoming arguments to memory.
-
leaf procedures: the procedures that don't call other procedures
-
Some optimizing compilers use interprocedural register allocation, analyzing all the functions in an entire program at once.
-
They assign different procedures different registers to receive parameters and hold local variables
-
Parameter x is a dead variable at the point where h(z) is called. Then f(x) can overwrite r1 without saving it.
-
Some architectures have register windows, so that each function invocation can allocate a fresh set of registers without memory traffic.
部分架构不会将寄存器放在栈帧中,会放在指定的寄存器中。针对叶子进程可以使用 interprocedural register allocation 进行优化。
Static Link
- Block Structure: In languages allowing nested function declarations (such as Pascal, ML, and Tiger), the inner functions may use variables declared in outer functions.
| JavaScript | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | |
此处例如 write 函数需要能够访问 prettyprint 的栈帧。Tiger 语言中需要通过 static link 来实现 Block structure。
static link:每当函数 f 被调用时,f 会被传递一个栈帧的指针,指向包含 f 的上一级函数,放置在 f 的 static link 的区域。如果是递归调用则传入自己的 static link。
上述代码详细的处理过程如下:
-
in show(0, tree); output -
passing pretryprint's own frame pointer (FP) as show's static link: prettyprint is the immediate enclosing function of show
-
show's static link = prettyprint's FP
-
function show(n:int, t: tree) = -
show stores its static link (the address of prettyprint's FP)
-
then indent(".") -
show calls indent, passing its own FP as indent's static link
-
show(n+1, t.left) -
show calls show, passing its own static link (not its own FP) as the static link
-
for i := 1 to n -
fetch n at an appropriate offset from indent's static link (which points at the frame of show)
-
write("\n") -
indent's static link (show's FP) + offset = show's static link = prettyprint's FP
-
How can indent use output from prettyprint's frame?
It starts with its own static link, then fetches show's, then fetches output.
Interm. Code 中间代码
2024.04.25
Three Address Code 三地址码
最基本的形式为 x = y op z 一条指令涉及到三个地址 ( 地址 )。对于复杂情况可以进行如下的拆解:
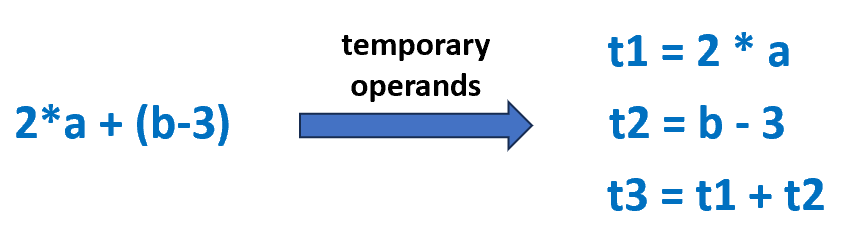
对于例如取负等操作需要特殊处理使其变为三地址码。
 |
 |
|---|---|
需要注意到其中例如 fact *= x 需要拆成两条指令来完成。使用 read 和 write 来进行 IO,使用 goto 进行跳转,halt 进行停机。
Intermediate Representation Tree
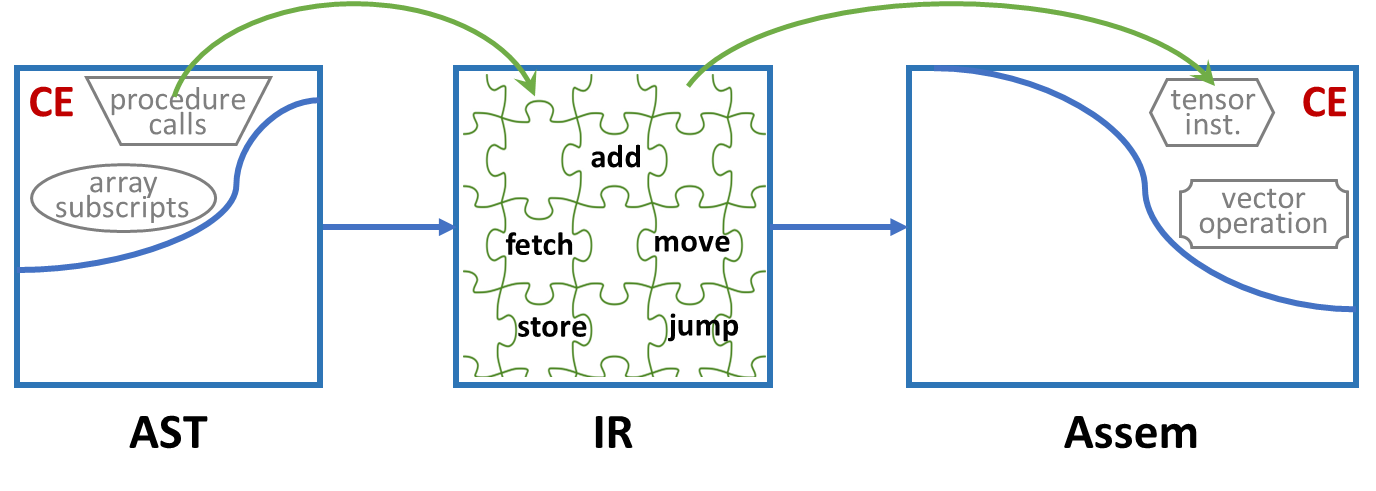
Expressions
IR 对 AST 进行简化,为翻译汇编代码提供方便。
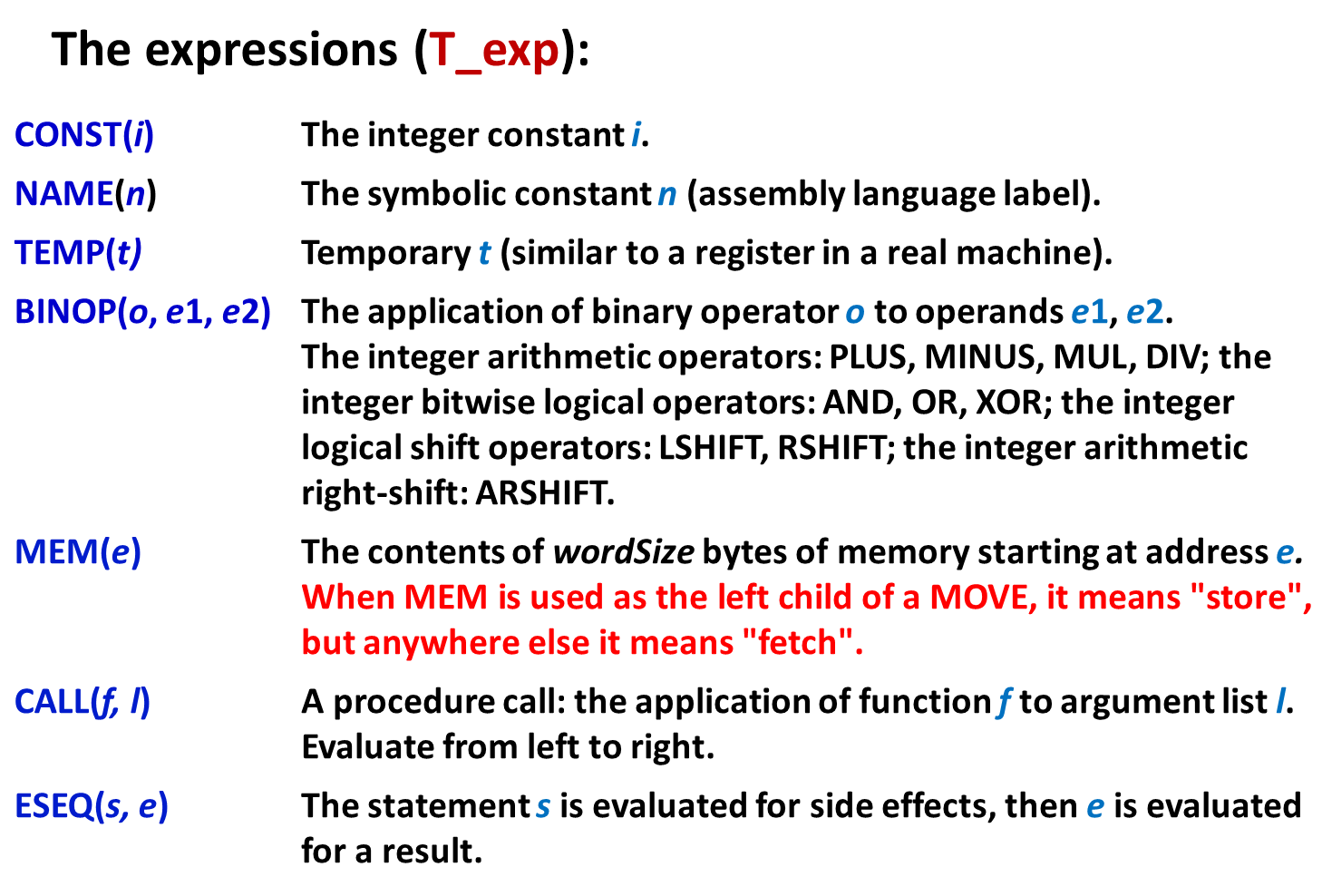
IR tree 并不是专为 Tiger 语言设计的,具有通用性。每个表达式都有返回值,存在一定的副作用。
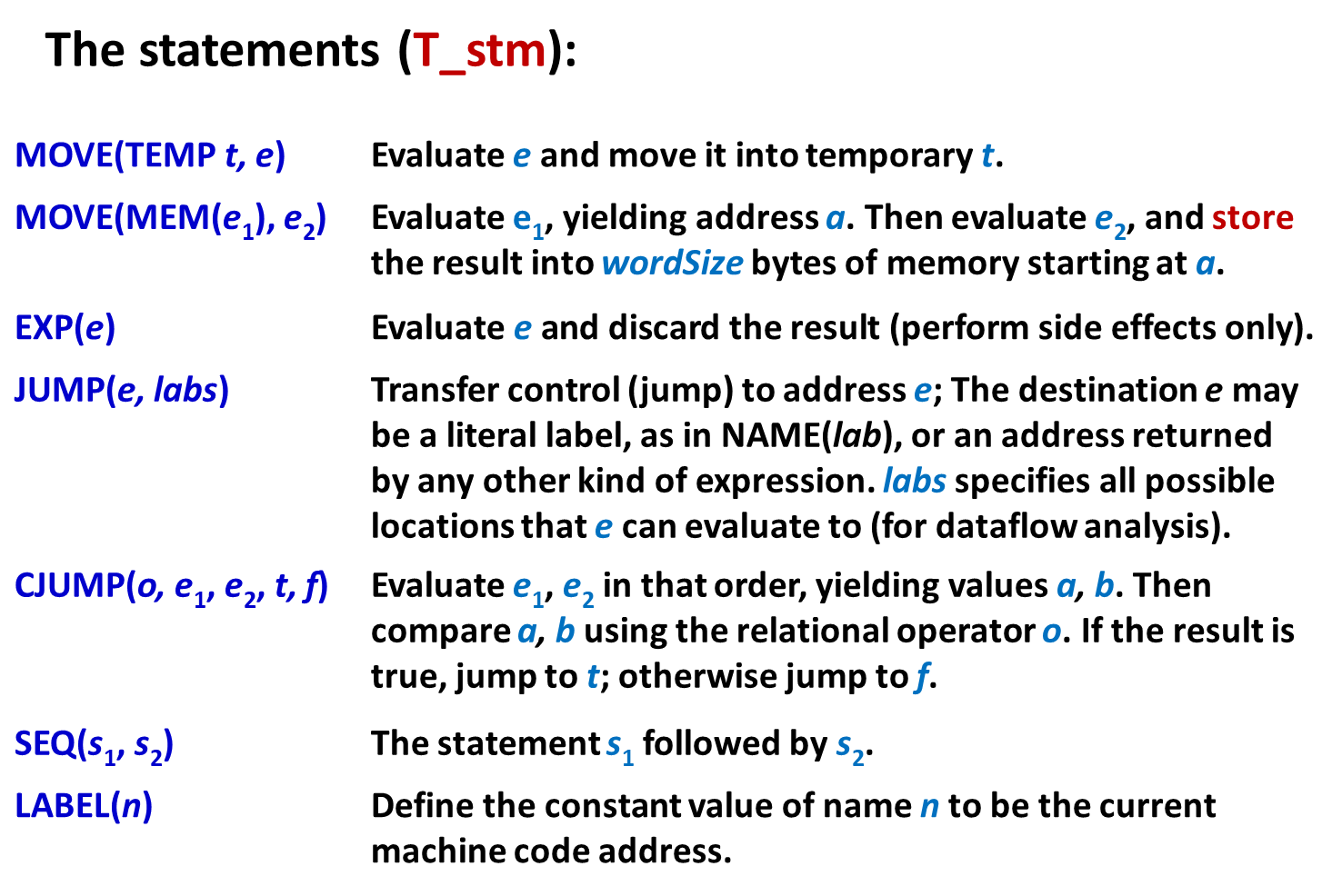
其中 EXP(e) 仅用作评估计算表达式的副作用 ( 寄存器改变 ) 等,不关心计算的结果。
语句部分是在评估副作用以及控制流,没有返回值。
Translate into IR tree
表达式分类:
Ex:有返回值,适合使用T_exp实现。Nx:没有返回值 ( 函数调用等 ),适合使用T_stm表达。Cx:特殊类型 ( 由于 Tiger 不支持布尔类型,故特殊处理 ),布尔表达式,使用 conditional jump (CJUMP) 与 Label 结合实现,举例如下: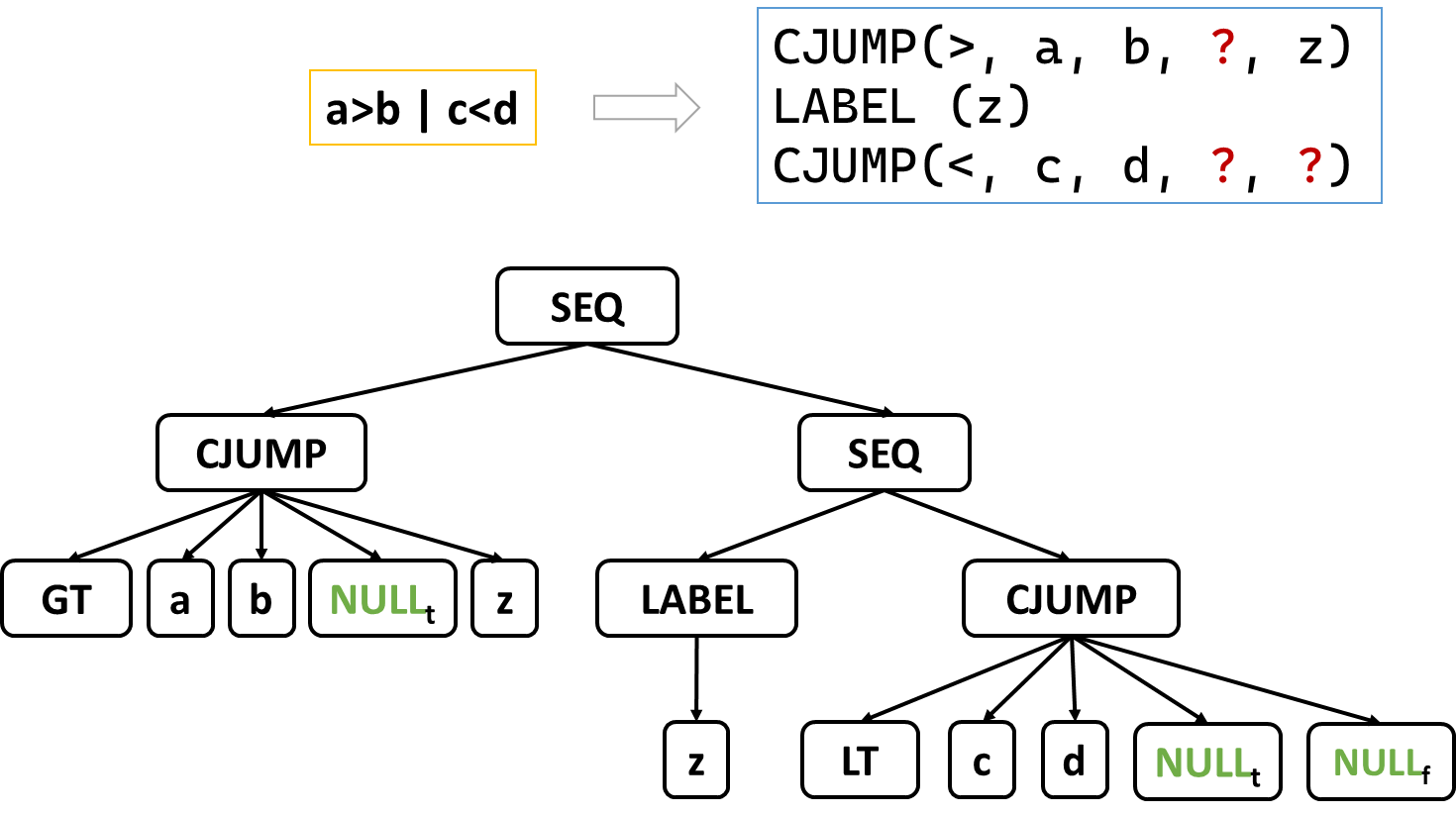
举例实现实现如下:
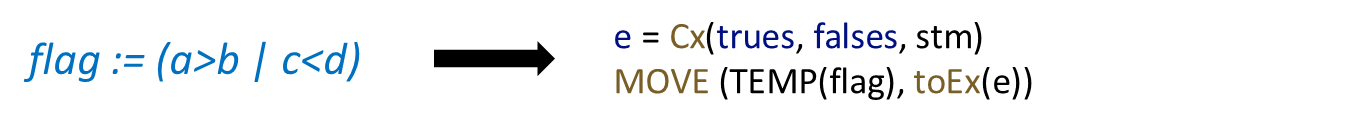
其中 Cx 的第一个参数表示为真执行的语句,toEx 大致实现如下:
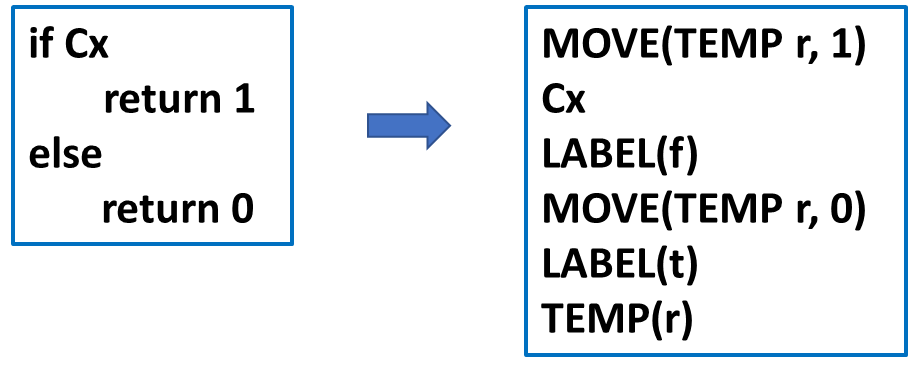
另一个例子如下:
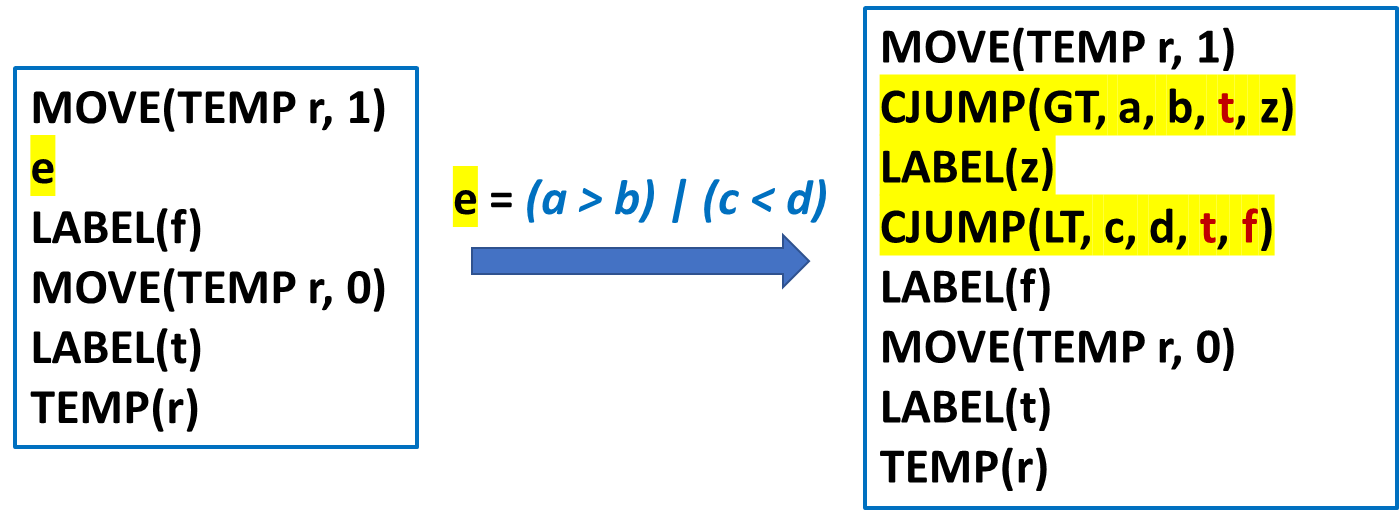
Simple Variables
对于变量的调用,过程如下:

其中 fp 指的是帧指针。
L-Values
表示的是内存的一个地址。
与之相对应的是右值,不表示能够被赋值的单元。
Scalar:标量,只用一个字长就能存储。
Tiger 语言中只有标量,但是在 C 等语言中,存在结构化的左值 ( 非标量 ),所以需要对 MEM 语句稍作修改:
| C | |
|---|---|
1 2 | |
Subscripting and Field Selection