密码学
整理
AES
2023 / 05 / 08
Advanced Encryption Standard
概况
AES 的密钥有 3 种:128 bit 循环轮数 10;192 bit 循环轮数 12;256 bit 循环轮数 14;
以 128 位 ( 16 字节 ) 密钥为例,设 p 为明文,k 为密钥,则 AES 的加密过程如下:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | |
数学基础
-
有限域:域 (field) 就是一个集合,我们可以在其上做加减乘除运算而不脱离该集合
-
有限域中元素的个数称为有限域的阶 (order)
- 有限域的阶必为素数 p 的幂 , 即 p n,其中 n 为正整数
-
对任意素数 p 和正整数 n,存在 p n 阶的有限域,记为 GF(p n )。当 n = 1 时,有限域 GF(p) 也称素域
-
例如 GF(2) 上有 2 个元素 0 和 1,加法定为异或,乘法定为与
-
再例如 GF(2 8 ) 对应 8 bit 的 2 进制数,加法就是按位异或 ( 可得出该域上 x 的加法逆元就是 x 本身,\(x \equiv -x\)),而对于乘法运算,举例以及代码如下:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
或者也可以用多项式的形式进行计算:
10001000 * 00000101 mod 0x11B => \(((x^7+x^3) * (x^2+1))\,mod\,(x^8+x^4+x^3+x+1)\)
MixColumn
| C | |
|---|---|
1 2 3 4 | |
\(\begin{bmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{bmatrix} \times \begin{bmatrix}4\\3\\2\\1\end{bmatrix} = \begin{bmatrix}14\\5\\0\\15\end{bmatrix} \stackrel{存储时需要将列转行}{\longrightarrow} \begin{bmatrix}14&5&0&15\end{bmatrix}\)
加密时,被乘数为 \(3\,1\,1\,2\) ,解密时将其乘法逆元 \(B\,D\,9\,E\),作为被乘数,将密文作为乘数,即可以还原出明文。
这里的乘法需要运用农夫算法进行处理。
RSA
2023 / 05 / 22
对称密码体制:加密和解密使用同一密钥。
RSA 算法采用公钥密码体制,也称非对称密码体制。
算法过程
- 选取两个大素数,p 和 q,计算乘积 \(n = p\,*\,q\),n 可以公开,p 和 q 保密。
- 随机选取加密密钥 e,使 e 和 \((p-1)*(q-1)\) 互质。
- 找出 d,使 \(e\,*\,d= 1\,mod\,((p-1)*(q-1))\)。
- 加密:\(c = m^e(mod\,n)\),解密:\(m = c^d(mod\,n)\)。
- (e, n) 作为公钥 ( 公开 ),(d, n) 作为私钥。
数学基础
Euler 函数:\(\phi(n)\) - 小于 n 且与 n 互素的整数个数。若 \(n_1,\,n_2\) 互素,则有 \(\phi(n_1*n_2) = \phi(n_1)*\phi(n_2)\)。此外有 \(\phi(n) = \prod_{p\,|\,n} (1-\frac{1}{p})\) 其中 p 为 可以整除 n ( 即下标 ) 的素数。
Euler 定理:若 \(gcd(x,\,n) = 1\),则 \(x^{\phi(n)} = 1 (mod \, n)\)
Fermat 小定理:可以由 Euler 定理得到,当 p 为素数时,有 \(\phi(p) = p-1\),故有 \(x^{p-1} = 1 (mod \, n)\)。
中国剩余定理:设 m 1 , m 2 , m 3 …, m r 两两互素 , 则以下同余方程组 x ≡ ai (mod mi), i = 1, 2, 3, …r 模 M = m 1 m 2 m 3 …m r 的唯一解为
\(x = \sum_{i = 1}^r a_i *M_i*(M_{i-1} \, mod \, m_i) \,mod\,M \,\,其中\, M_i = \frac{M}{m_i}\).
数字签名
发送方 A 给 接受方 B 发送信息 L。首先需要对信息进行加密。
信息加密的过程:1. (A) L' = RSA(L, B 的公钥 )。2. (B) L = RSA(L', B 的私钥 )。
为确认发送方为 A,需要进行数字签名。
数字签名的过程:1. (A) M = md5(L)。2. (A) M' = RSA(M, A 的私钥 )。3. (B) m = RSA(M', A 的公钥 ),比较 m 与 M 是否相同即可。
ECC
2023 / 06 / 05
椭圆曲线可以定义成所有满足方程 E: y 2 = x 3 + ax + b (mod p) 的点 (x, y) 所构成的集合。
若 x 3 + ax + b 没有重复的因式或 4a 3 + 27b 2 ≠ 0 ( 称为判别式 ),则 E: y 2 = x 3 + ax + b 能定义成为一个群。
数学基础
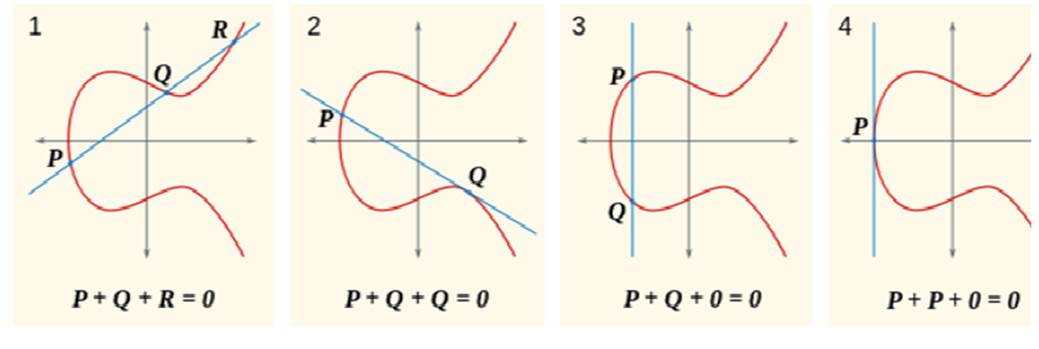
对于图 1 中,R 关于 x 轴的对称点 R' 于是有 P + Q = R'。其中所有点的横纵坐标都必须是整数。
(1) P + O = O + P = P
(2) 如果 P = (x 1 , y 1 ),Q = (x2, y2),且有 x 1 = x 2 及 y 1 = y 2 = 0,或有 x 1 = x 2 及 y 1 = -y 2 ≠ 0,则 P + Q = O;
(3) 如果 P = (x 1 , y 1 ),Q = (x2, y2),且排除 (1)(2),则 P + Q = (x 3 , y 3 ) 由下列规则决定:
x3 = λ2 - x1 - x2;y3 = λ(x1 - x3) - y1;当 P ≠ Q 时,λ = (y2 - y1) / (x2 - x1);当 P = Q 时,λ = (3x12 + a) / (2y1) ;
a,b,p,基点 G ( 满足曲线的某一点 ),G 的阶,余因子,六个概念决定了一条椭圆曲线。
n * G = 0 时称 n 是 G 的阶。1G,2G,...,nG 构成一个循环子群。(n + 1)G = 1G。满足曲线方程的所有点的个数称为曲线的阶。
余因子 = 曲线的阶 / G 的阶;